pcalc.presence
A Presence is a foundational concept in the presence calculus and this module includes all the concepts for modeling presence and the API to work with them.
Formally, a presence may represented as a 5-tuple:
$$ p = (e, b, t_0, t_1, m) $$
where:
- $e \in E \subseteq D$ is an element (thing) in the domain $D$,
- $b \in B \subseteq D$ is the boundary (place) in the domain $D$,
- $[t_0, t_1)$ is the half-open interval of presence in time.
- $m \in R$ is called the mass of the presence.
A presence can be viewed as a function:
$$ P: E \times B \times \overline{\mathbb{R}} \times \overline{\mathbb{R}} \to \mathbb{R} $$
where
- $P(e, b, t_0, t_1) = m \gt 0 $ if $e$ is present in $b$ during $[t_0, t_1)$
- $P(e, b, t_0, t_1) = 0 $ otherwise
When $m \in \{ 0,1 \} $ we get the simplest form of presence: a binary assertion. This is a statement that an element was present in a boundary for a continuous time interval (with mass = 1).
Presence mass is core concept that will be described in more detail shortly - for now, it is sufficient to think of it as a value or weight attached to a presence assertion that is derived from some function on the underlying domain that must be "measurable" in a precise mathematical sense.
The key thing is that the machinery of the presence calculus lets you work identically with binaru presences which are much more intutive and easy to understand, and presences derived on arbitrary measures. This generality gives us a great deal of power on reasoning about logical, desterministic/stochastic, linear/non-linear and complex adaptive systems using exactly the same set of tools.
Presence onset and reset
$t_0$ is called the onset time of the presence—the instant at which the presence transitions from zero to non-zero mass. $t_1$ is called the reset time — the instant at which the presence transitions back to zero.
We will say the presence is active over the half-open interval $[t_0, t_1)$ (meaning it includes $t_0$ but excludes $t_1$).
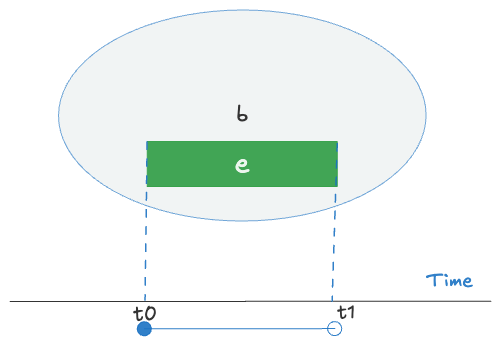
This diagram illustrates a presence assertion over a half-open interval $[t_0, t_1)$, where element $e$ is continuously present in boundary $b$ starting at $t_0$ (included) and ending just before $t_1$ (excluded).
The Open World Assumption
The time interval $[t_0, t_1)$ is defined over the extended reals $\overline{\mathbb{R}}$: the real line $\mathbb{R}$ extended with the symbols $-\infty$ and $+\infty$.
This reflects the presence calculus's open world assumption, which permits intervals that extend indefinitely into the past or future. A presence with $t_0 = -\infty$ represents a presence whose beginning is unknown, and $t_1 = +\infty$ represents a presence whose end is unknown.
Presences with both start and end unknown are valid and represent eternal presences. Many of the most interesting questions in the presence calculus involve reasoning about the dynamics of a domain under the epistemic uncertainty introduced by such presences.
Presence Assertions
A Presence Assertion is an assertion about the existence of a presence from the standpoint of a specific observer at a specific time.
A presence assertion is thus a seven-tuple $(e, b, t_0, t_1, m, o, t_2)$ where:
- $(e, b, t_0, t_1, m)$ is the presence being asserted,
- $o \in O \subseteq D$ is the observer (a domain entity), and
- $t_2 \in \overline{\mathbb{R}}$ is the assertion time.
Both observer and assertion time may themselves be unknown, and together they reflect the epistemic provenance of the assertion.
Given our open world assumptions, we assume by default that we are reasoning about dynamic sets of presences that reflect observations by various observers on the underlying domain. Presence assertions may be added or removed from this set, which in turn changes what we can say about the state of the domain. We assume (by construction, if necessary) that observers are part of the domain $D$.
For example, learning the reset time of a presence—when it was previously unknown—allows us to replace the old assertion with a new one that reflects greater epistemic certainty about the domain state. A new assertion may update the onset or reset time based on new information from different observers (e.g., sensor disagreements), reflecting the evolving nature of knowledge in an open world.
At any point in time, we are reasoning about a known subset of the domain's history, and potentially even making assertions about the future (estimates, forecasts, etc., which can also be modeled as presence assertions), each with its own epistemic status.
It is crucial to note that the presence calculus treats presence assertions as axiomatic: it does not question or infer their validity, nor does it make decisions based on provenance. However, the provenance of assertions may be used to reason about the reliability or implications of the conclusions reached via the machinery of the calculus.
For example, suppose in a traffic domain we observe that a vehicle (the element) crossed the 1-mile marker at 11:00 AM and the 2-mile marker at 11:10 AM. If we assert that the vehicle was continuously present (i.e., within the boundary between those markers) during the interval [11:00, 11:11), that assertion depends on domain-level assumptions—such as continuity of motion, absence of detours, or the nonexistence of teleportation.
In a different domain—for example, one in which a wormhole allows instantaneous travel between Mars and mile 1.6—such an assertion might be invalid.
The presence calculus does not attempt to resolve or validate such assumptions. It simply assumes that all presence assertions are logically valid according to domain semantics and proceeds to compute their consequences using the machinery of the calculus.
The key requirement though, is that the presence mass must be well defined. This brings us to the concept of a domain Signal over which presences are defined and asserted.
Domain Signals and Presence Mass
A Domain Signal is any function that varies over time and is associated with elements and boundaries in a given domain $D$. It may represent activity, value, demand, or any other observable quantity relevant to the system.
Let $$ F : (e, b, t) \to \mathbb{R}_{\geq 0} $$ be a function that assigns a non-negative value to each element–boundary–time triple. This is the general form of a domain signal in the Presence Calculus.
For the signal to be meaningful in the Presence Calculus, it must be measurable - that is, it must define a quantity that can be accumulated over time.
Measure theory and the Lebesgue measure provide the standard mathematical language to model such functions. In particular, the Lebesgue integral of the signal defines the presence mass: the total contribution it makes over a continuous time interval.
Integrability is the core requirement here—if a signal is Lebesgue integrable over an interval $[t_0, t_1)$, then its presence mass is well-defined and finite. This makes it possible to work with irregular, discontinuous, or sparse signals while still reasoning rigorously about accumulation and duration.
Given $(e, b, t_0, t_1)$, the presence mass is given by: $$ \mu_{e,b} = \int_{t_0}^{t_1} F(e, b, t)\, dt $$
This integral defines how much presence is accumulated over the interval for the given element–boundary pair, combining both the values of the function and how they are distributed over time.
This is not a particularly restrictive condition: the class of Lebesgue integrable functions is broad and includes most real-world signals encountered in practice. However, insisting that we use the Lebesgue integral to define mass over an interval (as opposed to, say, a statistical average) has meaningful consequences when modeling discontinuous signals. It ensures that the resulting "mass" retains its intended semantics as a presence measure, even as we apply more complex algebraic and topological operations to sets of presence assertions.
The Presence Calculus builds on this foundation, treating presence assertions as time-localized signals whose mass can be integrated, compared, and composed across boundaries.
In addition to integrability, a key property of a Lebesgue measure is that it must be finitely additive—that is, we must be able to compute sums over unions and intersections of sets of intervals.
Time as Topology
This brings us to a fundamental property of presences—and the key distinction between presences and point-in-time events: the continuity of presence gives us a natural and mathematically precise way to define a topology of presence over the extended real line $\overline{\mathbb{R}}$.
Each presence defines a basic open set in this topology, corresponding to its half-open interval $[t_0, t_1) \subset \overline{\mathbb{R}}.$ The collection of all such intervals forms a basis for a topology over time, using the standard technique from point-set topology of generating a topology from a basis of open sets. See BasisTopology for details.
This topological structure plays an important role in ensuring that presence mass is well-behaved under composition: it allows us to combine, intersect, and partition presences in ways that naturally satisfy the finite additivity conditions required for presence mass to behave like a Lebesgue measure.
This means that presence assertions allow us to reason about concepts such as nearness, overlap, continuity, and structure of presence in time— that is, how domain entities relate across time with mathematical precision.
It also allows us to compute sums, rates, averages, and other quantities across presences with well-defined semantics. This may seem like a technical detail, but it is essential: it allows us to handle sparse, discontinuous, bursty, or qualitative data with the same rigor as continuous signals.
The consequences of reasoning with presence assertions are temporal and topological: they give rise to notions of proximity, flow, and co-presence in time that reveal the shape, connectedness, and dynamics of the domain in mathematically precise ways.
With presence assertions, we can reason about patterns such as:
- elements that tend to be present together (co-presence),
- transitions between boundaries,
- regions of concentrated or evolving presence, and
- causal relationships between presences.
Furthermore, the Presence Calculus introduces certain topological invariants (see PresenceInvariant) that express general laws of conservation of presence mass.
This provides the foundational structure for reasoning about the dynamics and causality of presence in a domain.
Presence API
This module defines the data structure and associated methods for Presence, and serves as the canonical representation of presence assertions and their topological primitives in the presence calculus
Note: When interfacing with external systems that operate in wallclock time you will need to convert between timestamps and dates and floating point numbers when constructing presence assertions.
The TimeModel class (pcalc.time_model.TimeModel) is provided for this purpose.
1# -*- coding: utf-8 -*- 2# Copyright (c) 2025 Krishna Kumar 3# SPDX-License-Identifier: MIT 4""" 5A *Presence* is a foundational concept in the presence calculus and this module 6includes all the concepts for modeling presence and the API to work with them. 7 8Formally, a presence may represented as a 5-tuple: 9 10$$ 11p = (e, b, t_0, t_1, m) 12$$ 13 14where: 15- $e \in E \subseteq D$ is an element (thing) in the domain $D$, 16- $b \in B \subseteq D$ is the boundary (place) in the domain $D$, 17- $[t_0, t_1)$ is the half-open interval of presence in time. 18- $m \in R$ is called the 19<em>mass</em> of the presence. 20 21A presence can be viewed as a function: 22 23$$ 24P: E \\times B \\times \\overline{\\mathbb{R}} \\times \\overline{\\mathbb{R}} \\to \\mathbb{R} 25$$ 26 27 28where 29 30 31- $P(e, b, t_0, t_1) = m \gt 0 $ if $e$ is present in $b$ during $[t_0, t_1)$ 32- $P(e, b, t_0, t_1) = 0 $ otherwise 33 34 35When $m \in 36\\\\{ 0,1 \\\\} $ we get the simplest form of presence: a binary assertion. This is a statement that an element was 37present in a boundary for a continuous time interval (with mass = 1). 38 39Presence *mass* is core concept that 40will be described in more detail shortly - for now, it is sufficient to think of it as a value or weight attached to 41a presence assertion that is derived from some function on the underlying domain that must be "measurable" in a precise 42mathematical sense. 43 44The key thing is that the machinery of the presence calculus lets you work identically with binaru presences which are much more 45intutive and easy to understand, and presences derived on arbitrary measures. This generality gives us a great deal of power 46on reasoning about logical, desterministic/stochastic, linear/non-linear and complex adaptive systems using exactly the 47same set of tools. 48 49### Presence onset and reset 50 51$t_0$ is called the <em>onset time</em> of the presence—the instant at which the 52presence transitions from zero to non-zero mass. $t_1$ is called the *reset time* — 53the instant at which the presence transitions back to zero. 54 55We will say the presence is *active* 56over the half-open interval $[t_0, t_1)$ (meaning it 57includes $t_0$ but excludes $t_1$). 58 59<div style="text-align: center; margin: 2em 0;"> 60 <img src="../../assets/pcalc/half_open_presence.png" width="400px" /> 61 <div style="font-size: 0.9em; color: #555; margin-top: 0.5em;"> 62 Figure: A presence interval $[t_0, t_1)$ with $t_0$ included (●) and 63 $t_1$ excluded (○). 64 </div> 65</div> 66 67This diagram illustrates a presence assertion over a half-open interval 68$[t_0, t_1)$, where element $e$ is continuously present in boundary $b$ 69starting at $t_0$ (included) and ending just before $t_1$ (excluded). 70 71 72 73### The Open World Assumption 74 75The time interval $[t_0, t_1)$ is defined over the <em>extended</em> reals 76$\overline{\mathbb{R}}$: the real line $\mathbb{R}$ extended with the symbols 77$-\infty$ and $+\infty$. 78 79This reflects the presence calculus's open world assumption, which permits 80intervals that extend indefinitely into the past or future. A presence with 81$t_0 = -\infty$ represents a presence whose beginning is unknown, and 82$t_1 = +\infty$ represents a presence whose end is unknown. 83 84Presences with both start and end unknown are valid and represent eternal 85presences. Many of the most interesting questions in the presence calculus 86involve reasoning about the dynamics of a domain under the epistemic 87uncertainty introduced by such presences. 88 89--- 90### Presence Assertions 91 92A Presence Assertion is an assertion about the existence of a presence from 93the standpoint of a specific observer at a specific time. 94 95A presence assertion is thus a seven-tuple 96$(e, b, t_0, t_1, m, o, t_2)$ where: 97 98- $(e, b, t_0, t_1, m)$ is the presence being asserted, 99- $o \in O \subseteq D$ is the observer (a domain entity), and 100- $t_2 \in \overline{\mathbb{R}}$ is the assertion time. 101 102Both observer and assertion time may themselves be unknown, and together 103they reflect the epistemic *provenance* of the assertion. 104 105Given our open world assumptions, we assume by default that we are reasoning 106about *dynamic* sets of presences that reflect observations by various observers 107on the underlying domain. Presence assertions may be added or removed 108from this set, which in turn changes what we can say about the 109state of the domain. We assume (by construction, if necessary) that observers 110are part of the domain $D$. 111 112For example, learning the reset time of a presence—when it was previously 113unknown—allows us to replace the old assertion with a new one that reflects 114greater epistemic certainty about the domain state. A new assertion may update 115the onset or reset time based on new information from different observers 116(e.g., sensor disagreements), reflecting the evolving nature of knowledge in 117an open world. 118 119At any point in time, we are reasoning about a known subset of the domain's 120history, and potentially even making assertions about the *future* 121(estimates, forecasts, etc., which can also be modeled as presence assertions), 122each with its own epistemic status. 123 124It is crucial to note that the presence calculus treats presence assertions as 125*axiomatic*: it does not question or infer their validity, nor does it make 126decisions based on provenance. However, the provenance of assertions may be 127used to reason about the reliability or implications of the conclusions reached 128via the machinery of the calculus. 129 130For example, suppose in a traffic domain we observe that a vehicle (the 131element) crossed the 1-mile marker at 11:00 AM and the 2-mile marker at 13211:10 AM. If we assert that the vehicle was continuously present (i.e., 133within the boundary between those markers) during the interval [11:00, 11:11), 134that assertion depends on domain-level assumptions—such as continuity of 135motion, absence of detours, or the nonexistence of teleportation. 136 137In a different domain—for example, one in which a wormhole allows 138instantaneous travel between Mars and mile 1.6—such an assertion might be 139invalid. 140 141The presence calculus does *not* attempt to resolve or validate such 142assumptions. It simply assumes that all presence assertions are logically 143valid according to domain semantics and proceeds to compute their 144consequences using the machinery of the calculus. 145 146The key requirement though, is that the *presence mass* must be well defined. 147This brings us to the concept of a domain Signal over which presences are defined 148and asserted. 149 150### Domain Signals and Presence Mass 151 152A Domain Signal is any function that varies over time and is associated with 153elements and boundaries in a given domain $D$. It may represent activity, 154value, demand, or any other observable quantity relevant to the system. 155 156Let 157$$ 158F : (e, b, t) \\to \\mathbb{R}_{\\geq 0} 159$$ 160be a function that assigns a non-negative value to each element–boundary–time triple. 161This is the general form of a domain signal in the Presence Calculus. 162 163For the signal to be meaningful in the Presence Calculus, it must be *measurable* - 164that is, it must define a quantity that can be accumulated over time. 165 166*Measure theory* and the *Lebesgue measure* provide the standard mathematical language 167to model such functions. In particular, the *Lebesgue integral* of the signal 168defines the presence mass: the total contribution it makes over 169a continuous time interval. 170 171Integrability is the core requirement here—if a 172signal is Lebesgue integrable over an interval $[t_0, t_1)$, then its 173presence mass is well-defined and finite. This makes it possible to work with 174irregular, discontinuous, or sparse signals while still reasoning rigorously 175about accumulation and duration. 176 177Given $(e, b, t_0, t_1)$, the presence mass is given by: 178$$ 179\\mu_{e,b} = \\int_{t_0}^{t_1} F(e, b, t)\\, dt 180$$ 181 182This integral defines how much presence is accumulated over the interval for 183the given element–boundary pair, combining both the values of the function 184and how they are distributed over time. 185 186This is not a particularly restrictive condition: the class of Lebesgue integrable 187functions is broad and includes most real-world signals encountered in practice. 188However, insisting that we use the Lebesgue integral to define mass over an interval 189(as opposed to, say, a statistical average) has meaningful consequences when modeling 190discontinuous signals. It ensures that the resulting "mass" retains its intended semantics 191as a presence measure, even as we apply more complex algebraic and topological operations 192to sets of presence assertions. 193 194The Presence Calculus builds on this foundation, treating presence assertions 195as time-localized signals whose mass can be integrated, compared, and composed 196across boundaries. 197 198In addition to integrability, a key property of a Lebesgue measure is that it 199must be finitely additive—that is, we must be able to compute sums over 200unions and intersections of sets of intervals. 201 202### Time as Topology 203 204This brings us to a fundamental property of presences—and the key distinction 205between presences and point-in-time events: the continuity of presence gives us 206a natural and mathematically precise way to define a *topology* of presence 207over the extended real line $\overline{\\mathbb{R}}$. 208 209Each presence defines a basic open set in this topology, corresponding to its 210half-open interval $[t_0, t_1) \\subset \\overline{\\mathbb{R}}.$ The collection of 211all such intervals forms a basis for a topology over time, using the standard 212technique from point-set topology of generating a topology from a basis of 213open sets. See [BasisTopology](./basis_topology.html) for details. 214 215This topological structure plays an 216important role in ensuring that presence mass is well-behaved under composition: 217it allows us to combine, intersect, and partition presences in ways that 218naturally satisfy the finite additivity conditions required for presence mass 219to behave like a Lebesgue measure. 220 221This means that presence assertions allow us to reason about concepts such as 222*nearness*, *overlap*, *continuity*, and *structure* of presence in time— 223that is, how domain entities relate across time with mathematical precision. 224 225It also allows us to compute sums, rates, averages, and other quantities across 226presences with well-defined semantics. This may seem like a technical detail, 227but it is essential: it allows us to handle sparse, discontinuous, bursty, or 228qualitative data with the same rigor as continuous signals. 229 230The consequences of reasoning with presence assertions are *temporal* and *topological*: 231they give rise to notions of proximity, flow, and co-presence in time that reveal 232the shape, connectedness, and dynamics of the domain in mathematically precise ways. 233 234With presence assertions, we can reason about patterns such as: 235- elements that tend to be present together (*co-presence*), 236- transitions between boundaries, 237- regions of concentrated or evolving presence, and 238- causal relationships between presences. 239 240Furthermore, the Presence Calculus introduces certain topological invariants 241(see [PresenceInvariant](./presence_invariant_discrete.html)) that express 242general *laws of conservation of presence mass*. 243 244This provides the foundational structure for reasoning about the *dynamics* 245and *causality* of presence in a domain. 246 247--- 248 249## Presence API 250 251This module defines the data structure and associated methods for Presence, 252and serves as the canonical representation of presence assertions and their topological 253 primitives in the 254presence calculus 255 256Note: When interfacing with external systems that operate in wallclock time you will need to 257convert between timestamps and dates and floating point numbers when constructing presence assertions. 258 259The [TimeModel](./time_model.html) class (`pcalc.time_model.TimeModel`) is provided for this purpose. 260 261--- 262""" 263 264from __future__ import annotations 265from typing import Optional, Protocol, runtime_checkable 266 267from dataclasses import dataclass 268from typing import Optional, Callable 269 270from .entity import EntityProtocol 271 272 273PresenceFunction = Callable[[EntityProtocol, EntityProtocol, float], float] 274# Presence functions and Presence Protocols 275""" 276A `PresenceFunction` $f$ is a time-varying function represented as a callable of the form: 277 278```python 279(e: EntityProtocol, b: EntityProtocol, t: float) -> float 280``` 281 282It returns a real-valued signal that is non-zero only when $t$ falls within some half open 283interval $[t_s, t_e)$ 284 285Presence functions must satisfy the following property: 286 287- For some half-open interval $[t_s, t_e) in \overline{\mathbb{R}}$, the function is non-zero only within that interval: 288 289 - $f(e, b, t) \\\\ne 0$ only if $t \in [t_s, t_e)$ 290 - $f(e, b, t) = 0$ elsewhere 291 292The returned value for $f$ in $\mathbb{R}$ can represent any time-varying quantity that has meaning in the domain— 293such as revenue, attention, sensor signal strength, or value accrual. Note that since the function domain is over 294the extended reals, we do allow these presences to extend infinitely into the past and the future. 295 296For example, in a sales domain, if the element `e` is a customer and `b` is a customer segment, 297the presence function might represent revenue from that customer at time `t`. If $[t_s, t_e)$ 298represents the customer lifetime, then customer revenue is zero outside that interval. 299 300<div style="text-align: center; margin:2em"> 301 <img src="../../assets/pcalc/presence_function.png" width="600px" /> 302 <div style="font-size: 0.9em; color: #555; margin-top: 1em; margin-bottom: 1em;"> 303 Figure 1: A presence function for customer revenues in the sales domain. 304 </div> 305</div> 306 307Note that Inside the interval, the value may still drop to zero — presence does not 308require that every value for the presence function remain greater than zero during the interval. 309 310 311Here are more examples of presence functions in python. 312Note that `constant_presence` corresponds to the most commonly assumed form of 313presence in classical models. It represents entities with uniform presence 314over a finite interval—from the start of the event to its end—with constant 315instantaneous mass. 316 317Much of queueing theory and flow analysis is based solely on this simple 318model, where presence is modeled as a rectangular pulse with finite duration 319and constant density. 320 321The presence calculus generalizes this by allowing arbitrary real-valued 322functions with compact support over the extended real line 323$\\overline{\\mathbb{R}}$, enabling richer modeling of non-uniform, delayed, 324forecasted, or probabilistic presences. 325 326 327```python 328# Boolean presence: returns 1.0 within [start, end), 0.0 elsewhere 329def constant_presence(start: float, end: float) -> PresenceFunction: 330 def f(e, b, t): 331 return 1.0 if start <= t < end else 0.0 332 return f 333 334# Ramped presence: increases linearly from 0.0 to 1.0 over [start, end) 335def ramp_presence(start: float, end: float) -> PresenceFunction: 336 def f(e, b, t): 337 if start <= t < end: 338 return (t - start) / (end - start) 339 return 0.0 340 return f 341 342# Delayed pulse: returns fixed value only after a delay from start 343def delayed_presence(start: float, end: float, delay: float = 1.0) -> PresenceFunction: 344 def f(e, b, t): 345 if start + delay <= t < end: 346 return 1.0 347 return 0.0 348 return f 349``` 350 351These functions form the foundation of presence semantics. 352 353Presence functions are defined *in the domain* and serve as the bridge between discrete 354domain events and continuous presence intervals used in the presence calculus. 355They are exposed to the presence calculus via the `PresenceProtocol`. 356 357""" 358 359 360@runtime_checkable 361class PresenceProtocol(Protocol): 362 """ 363 The PresenceProtocol represents the contract between an arbitrary presence function 364 and the foo 365 """ 366 367 def __call__(self, t0: float, t1: float) -> float: ... 368 369 370 371 def overlaps(self, t0: float, t1: float) -> bool: ... 372 373 @property 374 def onset_time(self) -> float: ... 375 376 @property 377 def reset_time(self) -> float: ... 378 379 380@dataclass(frozen=True) 381class PresenceAssertion: 382 """ 383 384 This is the fundamental, immutable construct of The presence calculus, 385 and asserts the presence of an element at a boundary over a continuous interval of time. 386 387 A presence is defined over a half-open interval $[t_0, t_1)$ on the real 388 line, where $t_0$ is the onset time and $t_1$ is the reset time. 389 390 The 391 following constraints must hold: 392 393 - $t_0 < t_1$ 394 - $t_0 \\in \\mathbb{R} \\cup \\{-\\infty\\}$ 395 - $t_1 \\in \\mathbb{R} \\cup \\{+\\infty\\}$ 396 - $t_0 \\ne +\\infty$ 397 - $t_1 \\ne -\\infty$ 398 399 These rules ensure that the interval is well-formed, bounded on the left, 400 and open on the right. Intervals such as $[2.0, 5.0)$, $[-\\infty, 4.2)$, 401 and $[1.0, +\\infty)$ are allowed, as are the special case $[-\\infty, 402 +\\infty)$ and $[0,0),$ the empty presence. 403 404 With the empty presence as the only exception, intervals with zero or negative duration, or with reversed or 405 undefined bounds, are disallowed. 406 """ 407 element: Optional[EntityProtocol] 408 boundary: Optional[EntityProtocol] 409 onset_time: float 410 reset_time: float 411 presence: Optional[PresenceProtocol] = None 412 observer: Optional[EntityProtocol] | str = "observed" 413 assert_time: Optional[float] = 0.0 414 415 def __post_init__(self): 416 """ 417 Validates the temporal bounds of the presence interval 418 """ 419 if self.onset_time >= self.reset_time: 420 if not (self.onset_time == self.reset_time == 0): 421 raise ValueError( 422 f"Invalid interval: onset_time ({self.onset_time}) must be less than reset_time ({self.reset_time})") 423 424 if self.onset_time == float("inf"): 425 raise ValueError("Presence cannot begin at +inf") 426 427 if self.reset_time == float("-inf"): 428 raise ValueError("Presence cannot end at -inf") 429 430 def overlaps(self, t0: float, t1: float) -> bool: 431 return self.reset_time > t0 and self.onset_time < t1 432 433 def mass(self) -> float: 434 """ 435 Returns the mass of the presence. 436 437 438 439 """ 440 onset = max(0.0, self.onset_time) 441 return max(0.0, self.reset_time - onset) 442 443 def mass_contribution(self, t0: float, t1: float) -> float: 444 if t0 >= t1 or not self.overlaps(t0, t1): 445 return 0.0 446 start = max(self.onset_time, t0) 447 end = min(self.reset_time, t1) 448 return max(0.0, end - start) 449 450 def __str__(self) -> str: 451 element_str = str(self.element) if self.element is not None else "None" 452 boundary_str = str(self.boundary) if self.boundary is not None else "None" 453 interval_str = f"[{self.onset_time}, {self.reset_time})" 454 return ( 455 f"Presence(element={element_str}, boundary={boundary_str}, " 456 f"interval={interval_str}, provenance={self.observer})" 457 ) 458 459 460EMPTY_PRESENCE: PresenceAssertion = PresenceAssertion( 461 element=None, 462 boundary=None, 463 presence=None, 464 onset_time=0.0, 465 reset_time=0.0, 466 observer="empty", 467)
A PresenceFunction $f$ is a time-varying function represented as a callable of the form:
(e: EntityProtocol, b: EntityProtocol, t: float) -> float
It returns a real-valued signal that is non-zero only when $t$ falls within some half open interval $[t_s, t_e)$
Presence functions must satisfy the following property:
For some half-open interval $[t_s, t_e) in \overline{\mathbb{R}}$, the function is non-zero only within that interval:
- $f(e, b, t) \ne 0$ only if $t \in [t_s, t_e)$
- $f(e, b, t) = 0$ elsewhere
The returned value for $f$ in $\mathbb{R}$ can represent any time-varying quantity that has meaning in the domain— such as revenue, attention, sensor signal strength, or value accrual. Note that since the function domain is over the extended reals, we do allow these presences to extend infinitely into the past and the future.
For example, in a sales domain, if the element e is a customer and b is a customer segment,
the presence function might represent revenue from that customer at time t. If $[t_s, t_e)$
represents the customer lifetime, then customer revenue is zero outside that interval.
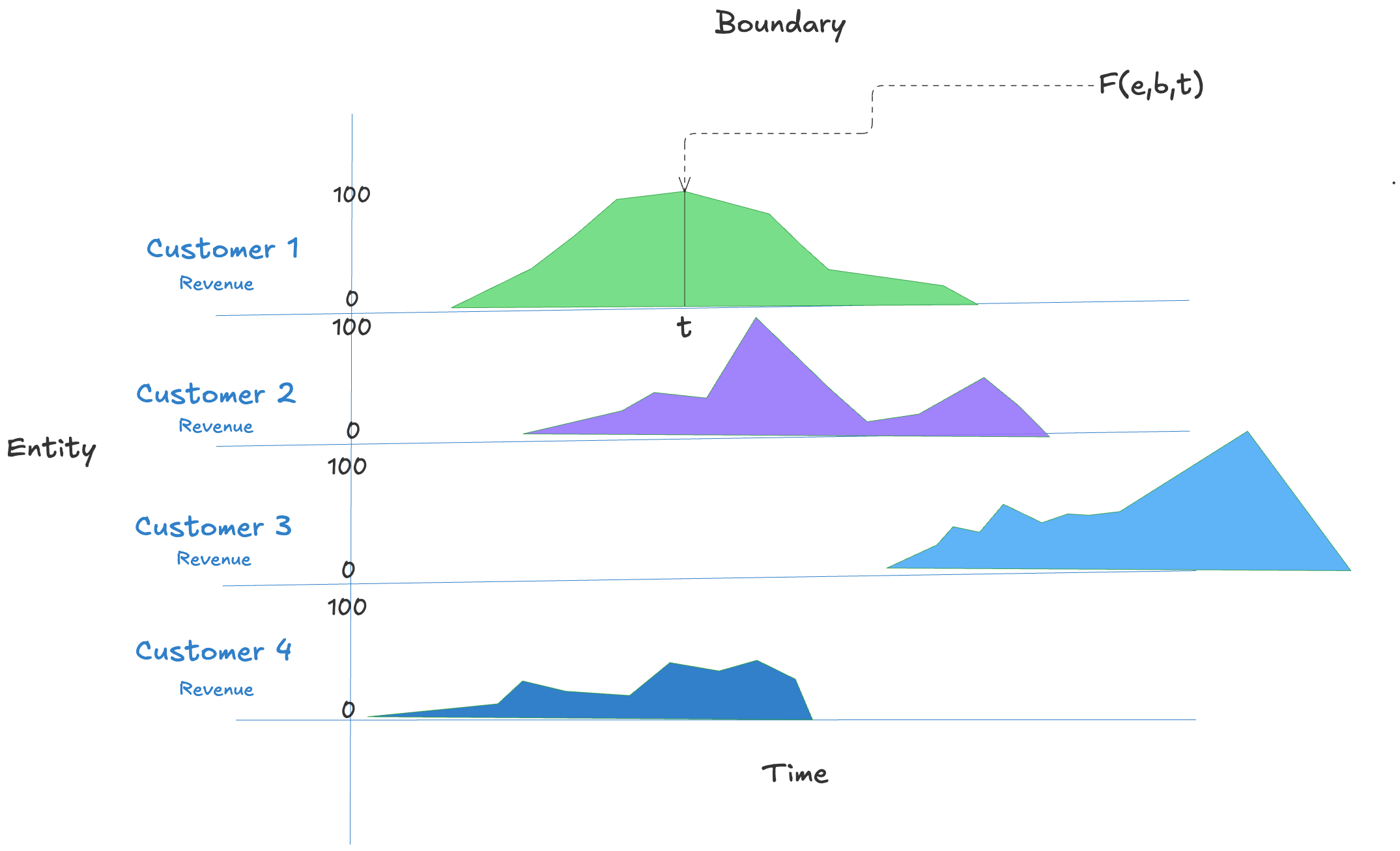
Note that Inside the interval, the value may still drop to zero — presence does not require that every value for the presence function remain greater than zero during the interval.
Here are more examples of presence functions in python.
Note that constant_presence corresponds to the most commonly assumed form of
presence in classical models. It represents entities with uniform presence
over a finite interval—from the start of the event to its end—with constant
instantaneous mass.
Much of queueing theory and flow analysis is based solely on this simple model, where presence is modeled as a rectangular pulse with finite duration and constant density.
The presence calculus generalizes this by allowing arbitrary real-valued functions with compact support over the extended real line $\overline{\mathbb{R}}$, enabling richer modeling of non-uniform, delayed, forecasted, or probabilistic presences.
# Boolean presence: returns 1.0 within [start, end), 0.0 elsewhere
def constant_presence(start: float, end: float) -> PresenceFunction:
def f(e, b, t):
return 1.0 if start <= t < end else 0.0
return f
# Ramped presence: increases linearly from 0.0 to 1.0 over [start, end)
def ramp_presence(start: float, end: float) -> PresenceFunction:
def f(e, b, t):
if start <= t < end:
return (t - start) / (end - start)
return 0.0
return f
# Delayed pulse: returns fixed value only after a delay from start
def delayed_presence(start: float, end: float, delay: float = 1.0) -> PresenceFunction:
def f(e, b, t):
if start + delay <= t < end:
return 1.0
return 0.0
return f
These functions form the foundation of presence semantics.
Presence functions are defined in the domain and serve as the bridge between discrete
domain events and continuous presence intervals used in the presence calculus.
They are exposed to the presence calculus via the PresenceProtocol.
361@runtime_checkable 362class PresenceProtocol(Protocol): 363 """ 364 The PresenceProtocol represents the contract between an arbitrary presence function 365 and the foo 366 """ 367 368 def __call__(self, t0: float, t1: float) -> float: ... 369 370 371 372 def overlaps(self, t0: float, t1: float) -> bool: ... 373 374 @property 375 def onset_time(self) -> float: ... 376 377 @property 378 def reset_time(self) -> float: ...
The PresenceProtocol represents the contract between an arbitrary presence function and the foo
1953def _no_init_or_replace_init(self, *args, **kwargs): 1954 cls = type(self) 1955 1956 if cls._is_protocol: 1957 raise TypeError('Protocols cannot be instantiated') 1958 1959 # Already using a custom `__init__`. No need to calculate correct 1960 # `__init__` to call. This can lead to RecursionError. See bpo-45121. 1961 if cls.__init__ is not _no_init_or_replace_init: 1962 return 1963 1964 # Initially, `__init__` of a protocol subclass is set to `_no_init_or_replace_init`. 1965 # The first instantiation of the subclass will call `_no_init_or_replace_init` which 1966 # searches for a proper new `__init__` in the MRO. The new `__init__` 1967 # replaces the subclass' old `__init__` (ie `_no_init_or_replace_init`). Subsequent 1968 # instantiation of the protocol subclass will thus use the new 1969 # `__init__` and no longer call `_no_init_or_replace_init`. 1970 for base in cls.__mro__: 1971 init = base.__dict__.get('__init__', _no_init_or_replace_init) 1972 if init is not _no_init_or_replace_init: 1973 cls.__init__ = init 1974 break 1975 else: 1976 # should not happen 1977 cls.__init__ = object.__init__ 1978 1979 cls.__init__(self, *args, **kwargs)
372 def overlaps(self, t0: float, t1: float) -> bool: ...
381@dataclass(frozen=True) 382class PresenceAssertion: 383 """ 384 385 This is the fundamental, immutable construct of The presence calculus, 386 and asserts the presence of an element at a boundary over a continuous interval of time. 387 388 A presence is defined over a half-open interval $[t_0, t_1)$ on the real 389 line, where $t_0$ is the onset time and $t_1$ is the reset time. 390 391 The 392 following constraints must hold: 393 394 - $t_0 < t_1$ 395 - $t_0 \\in \\mathbb{R} \\cup \\{-\\infty\\}$ 396 - $t_1 \\in \\mathbb{R} \\cup \\{+\\infty\\}$ 397 - $t_0 \\ne +\\infty$ 398 - $t_1 \\ne -\\infty$ 399 400 These rules ensure that the interval is well-formed, bounded on the left, 401 and open on the right. Intervals such as $[2.0, 5.0)$, $[-\\infty, 4.2)$, 402 and $[1.0, +\\infty)$ are allowed, as are the special case $[-\\infty, 403 +\\infty)$ and $[0,0),$ the empty presence. 404 405 With the empty presence as the only exception, intervals with zero or negative duration, or with reversed or 406 undefined bounds, are disallowed. 407 """ 408 element: Optional[EntityProtocol] 409 boundary: Optional[EntityProtocol] 410 onset_time: float 411 reset_time: float 412 presence: Optional[PresenceProtocol] = None 413 observer: Optional[EntityProtocol] | str = "observed" 414 assert_time: Optional[float] = 0.0 415 416 def __post_init__(self): 417 """ 418 Validates the temporal bounds of the presence interval 419 """ 420 if self.onset_time >= self.reset_time: 421 if not (self.onset_time == self.reset_time == 0): 422 raise ValueError( 423 f"Invalid interval: onset_time ({self.onset_time}) must be less than reset_time ({self.reset_time})") 424 425 if self.onset_time == float("inf"): 426 raise ValueError("Presence cannot begin at +inf") 427 428 if self.reset_time == float("-inf"): 429 raise ValueError("Presence cannot end at -inf") 430 431 def overlaps(self, t0: float, t1: float) -> bool: 432 return self.reset_time > t0 and self.onset_time < t1 433 434 def mass(self) -> float: 435 """ 436 Returns the mass of the presence. 437 438 439 440 """ 441 onset = max(0.0, self.onset_time) 442 return max(0.0, self.reset_time - onset) 443 444 def mass_contribution(self, t0: float, t1: float) -> float: 445 if t0 >= t1 or not self.overlaps(t0, t1): 446 return 0.0 447 start = max(self.onset_time, t0) 448 end = min(self.reset_time, t1) 449 return max(0.0, end - start) 450 451 def __str__(self) -> str: 452 element_str = str(self.element) if self.element is not None else "None" 453 boundary_str = str(self.boundary) if self.boundary is not None else "None" 454 interval_str = f"[{self.onset_time}, {self.reset_time})" 455 return ( 456 f"Presence(element={element_str}, boundary={boundary_str}, " 457 f"interval={interval_str}, provenance={self.observer})" 458 )
This is the fundamental, immutable construct of The presence calculus, and asserts the presence of an element at a boundary over a continuous interval of time.
A presence is defined over a half-open interval $[t_0, t_1)$ on the real line, where $t_0$ is the onset time and $t_1$ is the reset time.
The following constraints must hold:
- $t_0 < t_1$
- $t_0 \in \mathbb{R} \cup {-\infty}$
- $t_1 \in \mathbb{R} \cup {+\infty}$
- $t_0 \ne +\infty$
- $t_1 \ne -\infty$
These rules ensure that the interval is well-formed, bounded on the left, and open on the right. Intervals such as $[2.0, 5.0)$, $[-\infty, 4.2)$, and $[1.0, +\infty)$ are allowed, as are the special case $[-\infty, +\infty)$ and $[0,0),$ the empty presence.
With the empty presence as the only exception, intervals with zero or negative duration, or with reversed or undefined bounds, are disallowed.