pcalc
The Presence Calculus Toolkit
© 2025 Dr. Krishna Kumar SPDX-License-Identifier: MIT
Introduction
The Presence Calculus provides a mathematical formalism for reasoning about the relationship between measures on elements and boundaries in a domain over time.
It begins with the concept of a Presence—a measure over the real numbers, associated with a particular Element (thing) in a domain, observed within a Boundary (place), over a continuous interval of time.
Both Elements and Boundaries belong to an underlying domain $D$ under analysis.
Measure theory offers a general mechanism for representing both presence and its effects. This lets us model concepts such as value, impact, delay, cost, revenue, and user experience as forms of presence. It also enables rigorous reasoning about temporal constructs like time value, delayed value, and the option value of presence.
The Presence Calculus is built on rigorous mathematical foundations— measure theory and topology—anchored by presence as an epistemic primitive.
This frames each presence as an observation made by a specific observer at a specific time, within an open-world setting across an infinite timeline. It enables meaningful reasoning about complex systems where noise, delay, ambiguity, and the provenance of observations play a critical role.
Given a set of presence assertions over a domain $D$, the calculus provides rigorously defined primitives and constructs for analyzing element timelines and trajectories, presence-induced topologies on $D$, and the effects of co-presence—simultaneous element presence—within and across boundaries.#233
These techniques apply consistently across a wide range of domains, including stochastic, non-linear, adaptive, and complex systems.
Motivation
Our primary goal in developing the Presence Calculus is to support rigorous modeling and principled decision-making in complex, real-world domains. We aim to ensure that the use of data in such decisions rests on a foundation that is mathematically precise, logically coherent, and epistemically grounded.
The current state of measurement—particularly in messy, complex domains—is often deficient in all three of these areas. The Presence Calculus emerged from a search for better structural tools in contexts where traditional statistical or causal methods fall short.
Presence Calculus builds on ideas from measure theory and topology, and connects it stochastic process dynamics, queueing theory, and complex systems science—yet remains philosophically distinct from each of them in its focus. This allows it to connect disparate fields while re-framing their perspectives through the common epistemic lens of presence.
The foundational constructs of Presence Calculus allow us to define derived notions such as flow, stability, equilibrium, and coherence precisely, and to relate them to practically useful measures like delay, cost, revenue, and user experience—once interpreted within the semantics of the domain being modeled.
In messy, real-world domains, relationships between elements, boundaries, flows, and effects often emerge from complex, higher-dimensional interactions among many parameters. These patterns are often more amenable to machine analysis in high-dimensional representations than through the simplified, low-dimensional models we typically use to make decisions. The Presence Calculus lets us build such representations, starting from simple, declarative models of presence.
While we illustrate our ideas using real-world decision problems, our focus is not on prescribing what decisions to make or how to make them. That belongs to the application domain of Presence Calculus—a domain we believe is vast.
Our goal is to make this framework accessible enough for others to build powerful applications on top of it, without requiring a deep background in the underlying mathematics (though it will help in following some of the more technical arguments)
The Toolkit
The Presence Calculus Toolkit is a computationally efficient implementation of the core concepts and calculations in presence calculus.
This pcalc module in particular, is an elementary and accessible entry point to some of the more abstract
concepts in the presence calculus. It is a computational model for the calculus
capable of powering real-time analysis and simulation of complex systems. The module is designed as a lightweight,
easy-to-integrate analytical middleware library that connects real-time event streams, simulation models,
and static datasets from a domain to rich visualization and analysis tools.
While we'll provide several examples of end-to-end integrations, the library is open source under the MIT license, and you are encouraged to create models and applications—both commercial and non-commercial—that build on the concepts.
If you are comfortable learning by reading code and implementing models and don't mind just a tiny bit of formal mathematical notation, this is a better entry point to the presence calculus for you.
More background and general, informal discussion around these topics can be found on The Polaris Flow Dispatch.
Reading these docs
The documentation is organized so that you can get a very good idea of the scope of the presence calculus and it's implementation by reading the topics listed on the "submodules" left hand menu, in order.
Each module links to detailed API documentation that is also directly accessible from this page. The index is also searchable once you get familiar with the concepts.
We believe the space of potential applications is vast, and invite you to explore it—and to reach out if you have questions or would like to collaborate with me on helping develop it further.
1# -*- coding: utf-8 -*- 2# Copyright (c) 2025 Krishna Kumar 3# SPDX-License-Identifier: MIT 4 5""" 6#The Presence Calculus Toolkit 7© 2025 Dr. Krishna Kumar 8SPDX-License-Identifier: MIT 9 10## Introduction 11 12The Presence Calculus provides a mathematical formalism for reasoning about 13the relationship between measures on *elements* and *boundaries* in a domain over *time*. 14 15It begins with the concept of a Presence—a measure over the real numbers, associated with 16a particular *Element* (thing) in a domain, observed within a *Boundary* (place), 17over a continuous interval of time. 18 19Both Elements and Boundaries belong 20to an underlying domain $D$ under analysis. 21 22Measure theory offers a general mechanism for representing 23both presence and its effects. This lets us model concepts such as value, 24impact, delay, cost, revenue, and user experience as forms of presence. 25It also enables rigorous reasoning about temporal constructs like time value, 26delayed value, and the option value of presence. 27 28The Presence Calculus is built on rigorous mathematical foundations— 29measure theory and topology—anchored by presence as an epistemic primitive. 30 31This frames each presence as an observation made by a specific observer 32at a specific time, within an open-world setting across an infinite timeline. 33It enables meaningful reasoning about complex systems where 34noise, delay, ambiguity, and the provenance of observations play a critical role. 35 36Given a set of presence assertions over a domain $D$, the calculus provides 37rigorously defined primitives and constructs for analyzing element timelines 38and trajectories, presence-induced topologies on $D$, and the effects of 39co-presence—simultaneous element presence—within and across boundaries.#233 40 41 42These techniques apply consistently across a wide range of domains, including 43stochastic, non-linear, adaptive, and complex systems. 44 45<div style="text-align: center; margin:2em"> 46 <img src="../assets/pcalc/presence_calculus.svg" width="600px" /> 47 <div style="font-size: 0.9em; color: #555; margin-top: 1em; margin-bottom: 1em;"> 48 Figure 1: Key constructs—presences, element paths, presence matrix, and co-presence topology 49 </div> 50</div> 51 52## Motivation 53Our primary goal in developing the Presence Calculus is to support rigorous 54modeling and principled decision-making in complex, real-world domains. We aim 55to ensure that the use of data in such decisions rests on a foundation that is 56mathematically precise, logically coherent, and epistemically grounded. 57 58The current state of measurement—particularly in messy, complex domains—is often 59deficient in all three of these areas. The Presence Calculus emerged from a 60search for better structural tools in contexts where traditional statistical or 61causal methods fall short. 62 63Presence Calculus builds on ideas from measure theory and topology, and 64connects it stochastic process dynamics, queueing 65theory, and complex systems science—yet remains philosophically 66distinct from each of them in its focus. This allows it to connect disparate fields while 67re-framing their perspectives through the common epistemic lens of presence. 68 69The foundational constructs of Presence Calculus allow us to define derived 70notions such as flow, stability, equilibrium, and coherence precisely, and to 71relate them to practically useful measures like delay, cost, revenue, and user 72experience—once interpreted within the semantics of the domain being modeled. 73 74In messy, real-world domains, relationships between elements, boundaries, flows, 75and effects often emerge from complex, higher-dimensional interactions among 76many parameters. These patterns are often more amenable to machine analysis in 77high-dimensional representations than through the simplified, low-dimensional 78models we typically use to make decisions. The Presence Calculus lets us 79build such representations, starting from simple, declarative models of presence. 80 81While we illustrate our ideas using real-world decision problems, our focus is 82not on prescribing what decisions to make or how to make them. That belongs to 83the application domain of Presence Calculus—a domain we believe is vast. 84 85Our goal is to make this framework accessible enough for others to build powerful 86applications on top of it, without requiring a deep background in the 87underlying mathematics (though it will help in following some of the more technical 88arguments) 89 90## The Toolkit 91 92The Presence Calculus Toolkit is a computationally efficient implementation of the core concepts and 93calculations in presence calculus. 94 95This `pcalc` module in particular, is an elementary and accessible entry point to some of the more abstract 96concepts in the presence calculus. It is a computational model for the calculus 97capable of powering real-time analysis and simulation of complex systems. The module is designed as a lightweight, 98easy-to-integrate analytical middleware library that connects real-time event streams, simulation models, 99and static datasets from a domain to rich visualization and analysis tools. 100 101While we'll provide several examples of end-to-end integrations, the library is 102open source under the MIT license, and you are encouraged to create models and 103applications—both commercial and non-commercial—that build on the concepts. 104 105If you are comfortable learning by 106reading code and implementing models and don't mind just a tiny bit of 107formal mathematical notation, this is a better entry point to the presence calculus for you. 108 109More background and general, informal discussion around these topics 110can be found on [The Polaris Flow Dispatch.](https://wwww.polaris-flow-dispatch.com) 111 112## Reading these docs 113 114The documentation is organized so that you can get a very good idea of the 115scope of the presence calculus and it's implementation by reading the 116topics listed on the "submodules" left hand menu, in order. 117 118Each module 119links to detailed API documentation that is also directly accessible from this page. 120The index is also searchable once you get familiar with the concepts. 121 122We believe the space of potential 123applications is vast, and invite you to explore it—and to reach out if you 124have questions or would like to collaborate with me on helping develop it further. 125 126 127[Dr. Krishna Kumar](https://www.linkedin.com/in/krishnaku1/), 128<br> [The Polaris Advisor Program](https://github.com/polarisadvisor) 129 130 131""" 132 133from .entity import Entity, EntityProtocol 134from .presence import PresenceAssertion 135from .time_model import TimeModel 136from .basis_topology import BasisTopology 137from .presence_invariant import PresenceInvariant 138from .presence_matrix import PresenceMatrix 139from .time_scale import Timescale 140from .presence_map import PresenceMap 141from .presence_invariant_discrete import PresenceInvariantDiscrete 142 143__all__ = [ 144 # Domain API 145 "entity", 146 Entity, EntityProtocol, 147 148 "presence", 149 PresenceAssertion, 150 151 # Continuous Time Models 152 "time_model", 153 TimeModel, 154 "basis_topology", 155 BasisTopology, 156 "presence_invariant", 157 PresenceInvariant, 158 159 # Discrete Time Models 160 "time_scale", 161 Timescale, 162 "presence_map", 163 PresenceMap, 164 "presence_matrix", 165 PresenceMatrix, 166 "presence_invariant_discrete", 167 PresenceInvariantDiscrete, 168]
220class Entity(EntityMixin, EntityProtocol): 221 """A default implementation of fully functional entity. 222 223 ```python 224 elements = [ 225 Entity(id="cust-001", name="Alice Chen", metadata={"type": "customer"}), 226 Entity(id="cust-002", name="Bob Gupta", metadata={"type": "customer"}), 227 Entity(id="pros-003", name="Dana Rivera", metadata={"type": "prospect"}), 228 ] 229 boundaries = [ 230 Entity(id="seg-enterprise", name="Enterprise Segment", metadata={"region": "NA"}), 231 Entity(id="seg-smb", name="SMB Segment", metadata={"region": "EMEA"}), 232 Entity(id="seg-dormant", name="Flight Risk", metadata={"status": "inactive", "last login": "2024-06-01"}), 233 Entity(id="seg-prospect", name="Active Prospects", metadata={"status": "demo given"}) 234 ] 235 236 for e in elements: 237 print(f"Element: {e.summary()}") 238 239 for b in boundaries: 240 print(f"Boundary: {b.summary()}") 241 ``` 242 """ 243 __slots__ = ("_id", "_name", "_metadata") 244 245 # noinspection PyProtocol 246 def __init__(self, id: Optional[str] = None, name: Optional[str] = None, metadata: Optional[Dict[str, Any]] = None): 247 self._id: str = id or str(uuid.uuid4()) 248 self._name: str = name or self.id 249 self._metadata: Dict[str, Any] = metadata or {} 250 251 @property 252 def id(self) -> str: 253 return self._id 254 255 # noinspection PyProtocol 256 @property 257 def name(self) -> str: 258 return self._name 259 260 @name.setter 261 def name(self, name: str) -> None: 262 self._name = name 263 264 @property 265 def metadata(self) -> Dict[str, Any]: 266 return self._metadata 267 268 def __str__(self) -> str: 269 return self.summary()
A default implementation of fully functional entity.
elements = [
Entity(id="cust-001", name="Alice Chen", metadata={"type": "customer"}),
Entity(id="cust-002", name="Bob Gupta", metadata={"type": "customer"}),
Entity(id="pros-003", name="Dana Rivera", metadata={"type": "prospect"}),
]
boundaries = [
Entity(id="seg-enterprise", name="Enterprise Segment", metadata={"region": "NA"}),
Entity(id="seg-smb", name="SMB Segment", metadata={"region": "EMEA"}),
Entity(id="seg-dormant", name="Flight Risk", metadata={"status": "inactive", "last login": "2024-06-01"}),
Entity(id="seg-prospect", name="Active Prospects", metadata={"status": "demo given"})
]
for e in elements:
print(f"Element: {e.summary()}")
for b in boundaries:
print(f"Boundary: {b.summary()}")
A stable, unique identifier for the entity. Used for indexing and identity. Defaults to a uuid.uuid4().
Inherited Members
105@runtime_checkable 106class EntityProtocol(Protocol): 107 """ 108 The interface contract for a domain entity to participate in a presence assertion. 109 110 Each entity requires only a unique identifier, a user-facing name. 111 112 Optional metadata may be provided and exposes specific attributes of the domain 113 entities that are relevant when interpreting or manipulating the results 114 of an analysis using the machinery of the calculus. 115 116 See `Entity` for an example of a concrete implementation. 117 """ 118 __init__ = None # type: ignore 119 120 @property 121 def id(self) -> str: 122 """ 123 A stable, unique identifier for the entity. 124 Used for indexing and identity. 125 Defaults to a uuid.uuid4(). 126 """ 127 ... 128 129 @property 130 def name(self) -> str: 131 """ 132 A user facing name for the entity, defaults to the id if None. 133 """ 134 ... 135 136 @name.setter 137 def name(self, name: str) -> None: 138 """Setter for name""" 139 ... 140 141 @property 142 def metadata(self) -> Dict[str, Any]: 143 """ 144 Optional extensible key-value metadata. 145 """ 146 ...
The interface contract for a domain entity to participate in a presence assertion.
Each entity requires only a unique identifier, a user-facing name.
Optional metadata may be provided and exposes specific attributes of the domain entities that are relevant when interpreting or manipulating the results of an analysis using the machinery of the calculus.
See Entity for an example of a concrete implementation.
120 @property 121 def id(self) -> str: 122 """ 123 A stable, unique identifier for the entity. 124 Used for indexing and identity. 125 Defaults to a uuid.uuid4(). 126 """ 127 ...
A stable, unique identifier for the entity. Used for indexing and identity. Defaults to a uuid.uuid4().
381@dataclass(frozen=True) 382class PresenceAssertion: 383 """ 384 385 This is the fundamental, immutable construct of The presence calculus, 386 and asserts the presence of an element at a boundary over a continuous interval of time. 387 388 A presence is defined over a half-open interval $[t_0, t_1)$ on the real 389 line, where $t_0$ is the onset time and $t_1$ is the reset time. 390 391 The 392 following constraints must hold: 393 394 - $t_0 < t_1$ 395 - $t_0 \\in \\mathbb{R} \\cup \\{-\\infty\\}$ 396 - $t_1 \\in \\mathbb{R} \\cup \\{+\\infty\\}$ 397 - $t_0 \\ne +\\infty$ 398 - $t_1 \\ne -\\infty$ 399 400 These rules ensure that the interval is well-formed, bounded on the left, 401 and open on the right. Intervals such as $[2.0, 5.0)$, $[-\\infty, 4.2)$, 402 and $[1.0, +\\infty)$ are allowed, as are the special case $[-\\infty, 403 +\\infty)$ and $[0,0),$ the empty presence. 404 405 With the empty presence as the only exception, intervals with zero or negative duration, or with reversed or 406 undefined bounds, are disallowed. 407 """ 408 element: Optional[EntityProtocol] 409 boundary: Optional[EntityProtocol] 410 onset_time: float 411 reset_time: float 412 presence: Optional[PresenceProtocol] = None 413 observer: Optional[EntityProtocol] | str = "observed" 414 assert_time: Optional[float] = 0.0 415 416 def __post_init__(self): 417 """ 418 Validates the temporal bounds of the presence interval 419 """ 420 if self.onset_time >= self.reset_time: 421 if not (self.onset_time == self.reset_time == 0): 422 raise ValueError( 423 f"Invalid interval: onset_time ({self.onset_time}) must be less than reset_time ({self.reset_time})") 424 425 if self.onset_time == float("inf"): 426 raise ValueError("Presence cannot begin at +inf") 427 428 if self.reset_time == float("-inf"): 429 raise ValueError("Presence cannot end at -inf") 430 431 def overlaps(self, t0: float, t1: float) -> bool: 432 return self.reset_time > t0 and self.onset_time < t1 433 434 def mass(self) -> float: 435 """ 436 Returns the mass of the presence. 437 438 439 440 """ 441 onset = max(0.0, self.onset_time) 442 return max(0.0, self.reset_time - onset) 443 444 def mass_contribution(self, t0: float, t1: float) -> float: 445 if t0 >= t1 or not self.overlaps(t0, t1): 446 return 0.0 447 start = max(self.onset_time, t0) 448 end = min(self.reset_time, t1) 449 return max(0.0, end - start) 450 451 def __str__(self) -> str: 452 element_str = str(self.element) if self.element is not None else "None" 453 boundary_str = str(self.boundary) if self.boundary is not None else "None" 454 interval_str = f"[{self.onset_time}, {self.reset_time})" 455 return ( 456 f"Presence(element={element_str}, boundary={boundary_str}, " 457 f"interval={interval_str}, provenance={self.observer})" 458 )
This is the fundamental, immutable construct of The presence calculus, and asserts the presence of an element at a boundary over a continuous interval of time.
A presence is defined over a half-open interval $[t_0, t_1)$ on the real line, where $t_0$ is the onset time and $t_1$ is the reset time.
The following constraints must hold:
- $t_0 < t_1$
- $t_0 \in \mathbb{R} \cup {-\infty}$
- $t_1 \in \mathbb{R} \cup {+\infty}$
- $t_0 \ne +\infty$
- $t_1 \ne -\infty$
These rules ensure that the interval is well-formed, bounded on the left, and open on the right. Intervals such as $[2.0, 5.0)$, $[-\infty, 4.2)$, and $[1.0, +\infty)$ are allowed, as are the special case $[-\infty, +\infty)$ and $[0,0),$ the empty presence.
With the empty presence as the only exception, intervals with zero or negative duration, or with reversed or undefined bounds, are disallowed.
76class TimeModel: 77 78 79 def __init__(self, origin: datetime, unit: CalendarUnit = "seconds"): 80 self.origin = origin 81 self.unit = unit 82 83 def to_float(self, t: datetime) -> float: 84 delta = t - self.origin 85 seconds = delta.total_seconds() 86 87 if self.unit == "seconds": 88 return seconds 89 if self.unit == "minutes": 90 return seconds / 60.0 91 if self.unit == "hours": 92 return seconds / 3600.0 93 if self.unit == "days": 94 return delta.days + (delta.seconds / 86400.0) 95 if self.unit == "months": 96 return self._months_between(self.origin, t) 97 if self.unit == "quarters": 98 return self._months_between(self.origin, t) / 3.0 99 if self.unit == "years": 100 return self._months_between(self.origin, t) / 12.0 101 102 raise ValueError(f"Unsupported time unit: {self.unit}") 103 104 def from_float(self, t: float) -> datetime: 105 if self.unit == "seconds": 106 return self.origin + timedelta(seconds=t) 107 if self.unit == "minutes": 108 return self.origin + timedelta(minutes=t) 109 if self.unit == "hours": 110 return self.origin + timedelta(hours=t) 111 if self.unit == "days": 112 return self.origin + timedelta(days=t) 113 if self.unit in {"months", "quarters", "years"}: 114 months = { 115 "months": int(round(t)), 116 "quarters": int(round(t * 3)), 117 "years": int(round(t * 12)), 118 }[self.unit] 119 return self.origin + relativedelta(months=+months) 120 121 raise ValueError(f"Unsupported time unit: {self.unit}") 122 123 @staticmethod 124 def _months_between(d1: datetime, d2: datetime) -> float: 125 """Return the number of calendar months between two dates, fractional.""" 126 rd = relativedelta(d2, d1) 127 return rd.years * 12 + rd.months + (rd.days / 30.0)
83 def to_float(self, t: datetime) -> float: 84 delta = t - self.origin 85 seconds = delta.total_seconds() 86 87 if self.unit == "seconds": 88 return seconds 89 if self.unit == "minutes": 90 return seconds / 60.0 91 if self.unit == "hours": 92 return seconds / 3600.0 93 if self.unit == "days": 94 return delta.days + (delta.seconds / 86400.0) 95 if self.unit == "months": 96 return self._months_between(self.origin, t) 97 if self.unit == "quarters": 98 return self._months_between(self.origin, t) / 3.0 99 if self.unit == "years": 100 return self._months_between(self.origin, t) / 12.0 101 102 raise ValueError(f"Unsupported time unit: {self.unit}")
104 def from_float(self, t: float) -> datetime: 105 if self.unit == "seconds": 106 return self.origin + timedelta(seconds=t) 107 if self.unit == "minutes": 108 return self.origin + timedelta(minutes=t) 109 if self.unit == "hours": 110 return self.origin + timedelta(hours=t) 111 if self.unit == "days": 112 return self.origin + timedelta(days=t) 113 if self.unit in {"months", "quarters", "years"}: 114 months = { 115 "months": int(round(t)), 116 "quarters": int(round(t * 3)), 117 "years": int(round(t * 12)), 118 }[self.unit] 119 return self.origin + relativedelta(months=+months) 120 121 raise ValueError(f"Unsupported time unit: {self.unit}")
79class BasisTopology: 80 """ 81 The foundational topology generated by a set of presence assertions. 82 83 Presences are treated as basis elements defining basic open sets. 84 Internally, presences are grouped into sorted open covers per (element, boundary) 85 and exposed through join, closure, and overlap operations. 86 """ 87 88 def __init__(self, presences: Iterable[PresenceAssertion]) -> None: 89 """ 90 Initializes the topology from a set of presences. 91 92 Internally maintains a SortedSet for each (element, boundary) pair, 93 ordered by onset_time for efficient merge and overlap operations. 94 """ 95 self.cover_index: dict[Tuple, SortedSet[PresenceAssertion]] = defaultdict( 96 lambda: SortedSet(key=presence_sort_key) 97 ) 98 99 for p in presences: 100 key = (p.element, p.boundary) 101 self.cover_index[key].add(p) 102 103 def get_cover(self, element, boundary) -> SortedSet[PresenceAssertion]: 104 """ 105 Returns the open cover for a given (element, boundary) pair. 106 """ 107 return self.cover_index.get((element, boundary), SortedSet(key=presence_sort_key)) 108 109 @staticmethod 110 def join(p1: PresenceAssertion, p2: PresenceAssertion) -> PresenceAssertion: 111 """ 112 Returns the join of two basis elements if they overlap or touch in time. 113 Returns EMPTY_PRESENCE if the presences are disjoint or incompatible. 114 """ 115 if (p1.element, p1.boundary) != (p2.element, p2.boundary): 116 return EMPTY_PRESENCE 117 118 if p1.reset_time < p2.onset_time != float("-inf") and p1.reset_time != float("inf"): 119 return EMPTY_PRESENCE 120 if p2.reset_time < p1.onset_time != float("-inf") and p2.reset_time != float("inf"): 121 return EMPTY_PRESENCE 122 123 return PresenceAssertion( 124 element=p1.element, 125 boundary=p1.boundary, 126 onset_time=min(p1.onset_time, p2.onset_time), 127 reset_time=max(p1.reset_time, p2.reset_time), 128 observer="join", 129 ) 130 131 def closure(self) -> set[PresenceAssertion]: 132 """ 133 Computes the closure under join for each cover. 134 135 Returns a deduplicated set of merged presences that cover the same regions 136 as the original topology, but without adjacent overlaps. 137 """ 138 closed = set() 139 140 for key, cover in self.cover_index.items(): 141 merged_cover = [] 142 for p in cover: 143 if not merged_cover: 144 merged_cover.append(p) 145 continue 146 147 last = merged_cover[-1] 148 j = self.join(last, p) 149 150 if j is not EMPTY_PRESENCE: 151 merged_cover[-1] = j 152 else: 153 merged_cover.append(p) 154 155 closed.update(merged_cover) 156 157 return closed 158 159 def find_overlapping(self, presence: PresenceAssertion) -> list[PresenceAssertion]: 160 """ 161 Finds all presences in the same cover that overlap with the given presence. 162 163 This is a linear scan from the first potentially overlapping point onward, 164 relying on the sorted order of onset_time. 165 """ 166 key = (presence.element, presence.boundary) 167 cover = self.cover_index.get(key, SortedSet(key=presence_sort_key)) 168 overlapping = [] 169 170 for p in cover.irange(minimum=None, maximum=None): 171 if p.onset_time >= presence.reset_time: 172 break 173 if p.reset_time > presence.onset_time: 174 overlapping.append(p) 175 176 return overlapping 177 178 def __iter__(self): 179 for cover in self.cover_index.values(): 180 yield from cover
The foundational topology generated by a set of presence assertions.
Presences are treated as basis elements defining basic open sets. Internally, presences are grouped into sorted open covers per (element, boundary) and exposed through join, closure, and overlap operations.
88 def __init__(self, presences: Iterable[PresenceAssertion]) -> None: 89 """ 90 Initializes the topology from a set of presences. 91 92 Internally maintains a SortedSet for each (element, boundary) pair, 93 ordered by onset_time for efficient merge and overlap operations. 94 """ 95 self.cover_index: dict[Tuple, SortedSet[PresenceAssertion]] = defaultdict( 96 lambda: SortedSet(key=presence_sort_key) 97 ) 98 99 for p in presences: 100 key = (p.element, p.boundary) 101 self.cover_index[key].add(p)
Initializes the topology from a set of presences.
Internally maintains a SortedSet for each (element, boundary) pair, ordered by onset_time for efficient merge and overlap operations.
103 def get_cover(self, element, boundary) -> SortedSet[PresenceAssertion]: 104 """ 105 Returns the open cover for a given (element, boundary) pair. 106 """ 107 return self.cover_index.get((element, boundary), SortedSet(key=presence_sort_key))
Returns the open cover for a given (element, boundary) pair.
109 @staticmethod 110 def join(p1: PresenceAssertion, p2: PresenceAssertion) -> PresenceAssertion: 111 """ 112 Returns the join of two basis elements if they overlap or touch in time. 113 Returns EMPTY_PRESENCE if the presences are disjoint or incompatible. 114 """ 115 if (p1.element, p1.boundary) != (p2.element, p2.boundary): 116 return EMPTY_PRESENCE 117 118 if p1.reset_time < p2.onset_time != float("-inf") and p1.reset_time != float("inf"): 119 return EMPTY_PRESENCE 120 if p2.reset_time < p1.onset_time != float("-inf") and p2.reset_time != float("inf"): 121 return EMPTY_PRESENCE 122 123 return PresenceAssertion( 124 element=p1.element, 125 boundary=p1.boundary, 126 onset_time=min(p1.onset_time, p2.onset_time), 127 reset_time=max(p1.reset_time, p2.reset_time), 128 observer="join", 129 )
Returns the join of two basis elements if they overlap or touch in time. Returns EMPTY_PRESENCE if the presences are disjoint or incompatible.
131 def closure(self) -> set[PresenceAssertion]: 132 """ 133 Computes the closure under join for each cover. 134 135 Returns a deduplicated set of merged presences that cover the same regions 136 as the original topology, but without adjacent overlaps. 137 """ 138 closed = set() 139 140 for key, cover in self.cover_index.items(): 141 merged_cover = [] 142 for p in cover: 143 if not merged_cover: 144 merged_cover.append(p) 145 continue 146 147 last = merged_cover[-1] 148 j = self.join(last, p) 149 150 if j is not EMPTY_PRESENCE: 151 merged_cover[-1] = j 152 else: 153 merged_cover.append(p) 154 155 closed.update(merged_cover) 156 157 return closed
Computes the closure under join for each cover.
Returns a deduplicated set of merged presences that cover the same regions as the original topology, but without adjacent overlaps.
159 def find_overlapping(self, presence: PresenceAssertion) -> list[PresenceAssertion]: 160 """ 161 Finds all presences in the same cover that overlap with the given presence. 162 163 This is a linear scan from the first potentially overlapping point onward, 164 relying on the sorted order of onset_time. 165 """ 166 key = (presence.element, presence.boundary) 167 cover = self.cover_index.get(key, SortedSet(key=presence_sort_key)) 168 overlapping = [] 169 170 for p in cover.irange(minimum=None, maximum=None): 171 if p.onset_time >= presence.reset_time: 172 break 173 if p.reset_time > presence.onset_time: 174 overlapping.append(p) 175 176 return overlapping
Finds all presences in the same cover that overlap with the given presence.
This is a linear scan from the first potentially overlapping point onward, relying on the sorted order of onset_time.
11class PresenceInvariant: 12 """ 13 Computes the components of the Presence Invariant directly from a BasisTopology. 14 15 This invariant expresses a local conservation law of presence mass over any finite 16 time interval [t0, t1), using only the closure of the topology. 17 """ 18 19 def __init__(self, topology: BasisTopology): 20 self.topology = topology 21 self.closed_presences = topology.closure() 22 23 def _filter_window(self, t0: float, t1: float) -> list[PresenceAssertion]: 24 return [ 25 p for p in self.closed_presences 26 if p.overlaps(t0,t1) 27 ] 28 29 def get_presence_summary(self, t0: float, t1: float) -> Tuple[float, int, float]: 30 """ 31 Computes: 32 - Total presence mass A 33 - Number of overlapping presences N 34 - Interval length T 35 """ 36 if t0 >= t1: 37 return 0.0, 0, 0.0 38 39 A = 0.0 40 N = 0 41 T = t1 - t0 42 43 for p in self._filter_window(t0, t1): 44 r = p.mass_contribution(t0, t1) 45 if r > 0.0: 46 A += r 47 N += 1 48 49 return A, N, T 50 51 def avg_presence_density(self, t0: float, t1: float) -> float: 52 A, _, T = self.get_presence_summary(t0, t1) 53 return A / T if T > 0 else 0.0 54 55 def incidence_rate(self, t0: float, t1: float) -> float: 56 _, N, T = self.get_presence_summary(t0, t1) 57 return N / T if T > 0 else 0.0 58 59 60 def avg_presence_mass(self, t0: float, t1: float) -> float: 61 A, N, _ = self.get_presence_summary(t0, t1) 62 return A / N if N > 0 else 0.0 63 64 def invariant(self, t0: float, t1: float) -> Tuple[float, float, float]: 65 """ 66 Returns: 67 (avg_presence_density, incidence_rate, avg_presence_mass) 68 69 These satisfy the Presence Invariant: 70 avg_presence_density = incidence_rate × avg_presence_mass 71 """ 72 A, N, T = self.get_presence_summary(t0, t1) 73 L = A / T if T > 0 else 0.0 74 Λ = N / T if T > 0 else 0.0 75 w = A / N if N > 0 else 0.0 76 return L, Λ, w
Computes the components of the Presence Invariant directly from a BasisTopology.
This invariant expresses a local conservation law of presence mass over any finite time interval [t0, t1), using only the closure of the topology.
29 def get_presence_summary(self, t0: float, t1: float) -> Tuple[float, int, float]: 30 """ 31 Computes: 32 - Total presence mass A 33 - Number of overlapping presences N 34 - Interval length T 35 """ 36 if t0 >= t1: 37 return 0.0, 0, 0.0 38 39 A = 0.0 40 N = 0 41 T = t1 - t0 42 43 for p in self._filter_window(t0, t1): 44 r = p.mass_contribution(t0, t1) 45 if r > 0.0: 46 A += r 47 N += 1 48 49 return A, N, T
Computes:
- Total presence mass A
- Number of overlapping presences N
- Interval length T
64 def invariant(self, t0: float, t1: float) -> Tuple[float, float, float]: 65 """ 66 Returns: 67 (avg_presence_density, incidence_rate, avg_presence_mass) 68 69 These satisfy the Presence Invariant: 70 avg_presence_density = incidence_rate × avg_presence_mass 71 """ 72 A, N, T = self.get_presence_summary(t0, t1) 73 L = A / T if T > 0 else 0.0 74 Λ = N / T if T > 0 else 0.0 75 w = A / N if N > 0 else 0.0 76 return L, Λ, w
Returns:
(avg_presence_density, incidence_rate, avg_presence_mass)
These satisfy the Presence Invariant:
avg_presence_density = incidence_rate × avg_presence_mass
13@dataclass 14class Timescale: 15 """ 16 Timescale represents a partitioning of a continuous time interval [t0, t1) 17 into N = ceil((t1 - t0) / bin_width) contiguous, left-aligned, non-overlapping bins. 18 19 Each bin has width `bin_width` and covers a half-open interval: 20 Bin k = [t0 + k * bin_width, t0 + (k + 1) * bin_width) 21 22 This class provides methods for: 23 - Mapping real-valued timestamps to discrete bin indices 24 - Extracting the time boundaries of any bin 25 - Computing which bins an interval [start, end) overlaps 26 - Estimating how much of a bin is covered by a given interval 27 28 **Boundary Behavior**: 29 - All bins lie strictly within [t0, t1) 30 - Any time `t` where t < t0 or t >= t1 is considered **outside** the defined timescale 31 - bin_index(t) may return an out-of-range index if `t < t0` or `t >= t1` 32 33 This class does not perform clipping: it assumes all inputs are in-range unless explicitly clipped by the caller. 34""" 35 36 t0: float 37 """start time of the interval [t0, t1)""" 38 t1: float 39 """end time of the interval [t0, t1)""" 40 41 bin_width: float 42 """Width of each bin""" 43 44 @property 45 def num_bins(self) -> int: 46 """Return number of bins between t0 and t1.""" 47 return int(np.ceil((self.t1 - self.t0) / self.bin_width)) 48 49 # Mapping from continuous time to discrete bins. 50 def bin_index(self, time: float) -> int: 51 """Purpose: 52 Map a real-valued timestamp to the index of the bin that contains it. 53 54 Contract: 55 Returns k such that bin_start(k) ≤ time < bin_end(k) 56 Uses floor() logic — i.e., left-aligned binning 57 No bounds check: time < t0 may yield negative indices; time ≥ t1 may return out-of-bounds indices 58 Caller is responsible for ensuring t0 ≤ time < t1 if range enforcement is needed 59 """ 60 return int(np.floor((time - self.t0) / self.bin_width)) 61 62 def bin_slice(self, start: float, end: float) -> Tuple[int, int]: 63 """Return the bin indices [start_bin, end_bin) that overlap the interval [start, end). 64 Contract: 65 - Clips the interval [start, end) to [t0, t1) before binning 66 - Computes: 67 start_bin = floor((clipped_start - t0) / bin_width) 68 end_bin = ceil((clipped_end - t0) / bin_width) 69 - Resulting slice [start_bin, end_bin) may be empty if the interval does not overlap the timescale 70 - start_bin ∈ [0, num_bins) 71 - end_bin ∈ [0, num_bins] 72 73 """ 74 effective_start = max(start, self.t0) 75 effective_end = min(end, self.t1) 76 if effective_start >= effective_end: 77 return 0, 0 78 start_bin = int(np.floor((effective_start - self.t0) / self.bin_width)) 79 end_bin = int(np.ceil((effective_end - self.t0) / self.bin_width)) 80 return start_bin, end_bin 81 82 def fractional_overlap(self, start: float, end: float, bin_idx: int) -> float: 83 """Return the fraction of the bin at index `bin_idx` that is covered by the interval [start, end). 84 Contract: 85 - Computes how much of bin_idx's interval is covered by [start, end) 86 - Returns value in [0.0, 1.0] based on normalized overlap over bin width 87 - Clipped to bin extent: overlaps outside the bin are ignored 88 - Used to compute partial presence contribution within a bin 89 """ 90 # Clip to timescale 91 start = max(start, self.t0) 92 end = min(end, self.t1) 93 94 bin_start = self.bin_start(bin_idx) 95 bin_end = self.bin_end(bin_idx) 96 97 overlap_start = max(start, bin_start) 98 overlap_end = min(end, bin_end) 99 100 return max(0.0, overlap_end - overlap_start) / self.bin_width 101 102 # Mapping from discrete bins back to continuous time. 103 def bin_start(self, bin_idx: int) -> float: 104 """Return the start time of a bin given its index. 105 Contract: 106 bin_start(k) = t0 + k * bin_width 107 """ 108 return self.t0 + bin_idx * self.bin_width 109 110 def bin_end(self, bin_idx: int) -> float: 111 """Return the end time of a bin given its index. 112 Contract: 113 bin_end(k) = t0 + (k + 1) * bin_width 114 """ 115 return self.t0 + (bin_idx + 1) * self.bin_width 116 117 def bin_edges(self) -> np.ndarray: 118 """ 119 Return an array of bin edge times from t0 to t1, spaced by bin_width. 120 121 The result has length `num_bins + 1` and is safe against floating-point rounding 122 by capping the range to include exactly the number of bins implied by `num_bins()`. 123 124 Contract: 125 - Returns `num_bins + 1` edge values such that: 126 edges = [t0, t0 + bin_width, ..., t1] 127 128 - Guarantees: 129 bin_start(k) == edges[k] 130 bin_end(k) == edges[k + 1] 131 132 - Handles floating-point rounding safely: 133 If np.arange overproduces due to rounding, result is trimmed 134 to ensure exactly `num_bins + 1` entries. 135 136 This method defines the canonical bin boundaries used across 137 the presence matrix and all derived metrics. 138 139 Example: 140 Timescale(t0=0.0, t1=10.0, bin_width=2.0).bin_edges() 141 => array([0.0, 2.0, 4.0, 6.0, 8.0, 10.0]) 142 """ 143 num_edges = self.num_bins + 1 144 edges = np.arange(self.t0, self.t0 + num_edges * self.bin_width, self.bin_width) 145 146 # Ensure exactly num_edges (for safety in rare floating-point cases) 147 if len(edges) > num_edges: 148 edges = edges[:num_edges] 149 return edges 150 151 152 def time_range(self, bin_idx: int) -> Tuple[float, float]: 153 """ 154 Return the (start, end) time of a bin. 155 Contract: 156 Returns tuple (bin_start(k), bin_end(k)) 157 Matches exactly the continuous interval spanned by the bin 158 """ 159 return self.bin_start(bin_idx), self.bin_end(bin_idx)
Timescale represents a partitioning of a continuous time interval [t0, t1) into N = ceil((t1 - t0) / bin_width) contiguous, left-aligned, non-overlapping bins.
Each bin has width bin_width and covers a half-open interval:
Bin k = [t0 + k * bin_width, t0 + (k + 1) * bin_width)
This class provides methods for:
- Mapping real-valued timestamps to discrete bin indices
- Extracting the time boundaries of any bin
- Computing which bins an interval [start, end) overlaps
- Estimating how much of a bin is covered by a given interval
Boundary Behavior:
- All bins lie strictly within [t0, t1)
- Any time
twhere t < t0 or t >= t1 is considered outside the defined timescale - bin_index(t) may return an out-of-range index if
t < t0ort >= t1
This class does not perform clipping: it assumes all inputs are in-range unless explicitly clipped by the caller.
44 @property 45 def num_bins(self) -> int: 46 """Return number of bins between t0 and t1.""" 47 return int(np.ceil((self.t1 - self.t0) / self.bin_width))
Return number of bins between t0 and t1.
50 def bin_index(self, time: float) -> int: 51 """Purpose: 52 Map a real-valued timestamp to the index of the bin that contains it. 53 54 Contract: 55 Returns k such that bin_start(k) ≤ time < bin_end(k) 56 Uses floor() logic — i.e., left-aligned binning 57 No bounds check: time < t0 may yield negative indices; time ≥ t1 may return out-of-bounds indices 58 Caller is responsible for ensuring t0 ≤ time < t1 if range enforcement is needed 59 """ 60 return int(np.floor((time - self.t0) / self.bin_width))
Purpose:
Map a real-valued timestamp to the index of the bin that contains it.
Contract:
Returns k such that bin_start(k) ≤ time < bin_end(k) Uses floor() logic — i.e., left-aligned binning No bounds check: time < t0 may yield negative indices; time ≥ t1 may return out-of-bounds indices Caller is responsible for ensuring t0 ≤ time < t1 if range enforcement is needed
62 def bin_slice(self, start: float, end: float) -> Tuple[int, int]: 63 """Return the bin indices [start_bin, end_bin) that overlap the interval [start, end). 64 Contract: 65 - Clips the interval [start, end) to [t0, t1) before binning 66 - Computes: 67 start_bin = floor((clipped_start - t0) / bin_width) 68 end_bin = ceil((clipped_end - t0) / bin_width) 69 - Resulting slice [start_bin, end_bin) may be empty if the interval does not overlap the timescale 70 - start_bin ∈ [0, num_bins) 71 - end_bin ∈ [0, num_bins] 72 73 """ 74 effective_start = max(start, self.t0) 75 effective_end = min(end, self.t1) 76 if effective_start >= effective_end: 77 return 0, 0 78 start_bin = int(np.floor((effective_start - self.t0) / self.bin_width)) 79 end_bin = int(np.ceil((effective_end - self.t0) / self.bin_width)) 80 return start_bin, end_bin
Return the bin indices [start_bin, end_bin) that overlap the interval [start, end).
Contract:
- Clips the interval [start, end) to [t0, t1) before binning
- Computes: start_bin = floor((clipped_start - t0) / bin_width) end_bin = ceil((clipped_end - t0) / bin_width)
- Resulting slice [start_bin, end_bin) may be empty if the interval does not overlap the timescale
- start_bin ∈ [0, num_bins)
- end_bin ∈ [0, num_bins]
82 def fractional_overlap(self, start: float, end: float, bin_idx: int) -> float: 83 """Return the fraction of the bin at index `bin_idx` that is covered by the interval [start, end). 84 Contract: 85 - Computes how much of bin_idx's interval is covered by [start, end) 86 - Returns value in [0.0, 1.0] based on normalized overlap over bin width 87 - Clipped to bin extent: overlaps outside the bin are ignored 88 - Used to compute partial presence contribution within a bin 89 """ 90 # Clip to timescale 91 start = max(start, self.t0) 92 end = min(end, self.t1) 93 94 bin_start = self.bin_start(bin_idx) 95 bin_end = self.bin_end(bin_idx) 96 97 overlap_start = max(start, bin_start) 98 overlap_end = min(end, bin_end) 99 100 return max(0.0, overlap_end - overlap_start) / self.bin_width
Return the fraction of the bin at index bin_idx that is covered by the interval [start, end).
Contract:
- Computes how much of bin_idx's interval is covered by [start, end)
- Returns value in [0.0, 1.0] based on normalized overlap over bin width
- Clipped to bin extent: overlaps outside the bin are ignored
- Used to compute partial presence contribution within a bin
103 def bin_start(self, bin_idx: int) -> float: 104 """Return the start time of a bin given its index. 105 Contract: 106 bin_start(k) = t0 + k * bin_width 107 """ 108 return self.t0 + bin_idx * self.bin_width
Return the start time of a bin given its index.
Contract:
bin_start(k) = t0 + k * bin_width
110 def bin_end(self, bin_idx: int) -> float: 111 """Return the end time of a bin given its index. 112 Contract: 113 bin_end(k) = t0 + (k + 1) * bin_width 114 """ 115 return self.t0 + (bin_idx + 1) * self.bin_width
Return the end time of a bin given its index.
Contract:
bin_end(k) = t0 + (k + 1) * bin_width
117 def bin_edges(self) -> np.ndarray: 118 """ 119 Return an array of bin edge times from t0 to t1, spaced by bin_width. 120 121 The result has length `num_bins + 1` and is safe against floating-point rounding 122 by capping the range to include exactly the number of bins implied by `num_bins()`. 123 124 Contract: 125 - Returns `num_bins + 1` edge values such that: 126 edges = [t0, t0 + bin_width, ..., t1] 127 128 - Guarantees: 129 bin_start(k) == edges[k] 130 bin_end(k) == edges[k + 1] 131 132 - Handles floating-point rounding safely: 133 If np.arange overproduces due to rounding, result is trimmed 134 to ensure exactly `num_bins + 1` entries. 135 136 This method defines the canonical bin boundaries used across 137 the presence matrix and all derived metrics. 138 139 Example: 140 Timescale(t0=0.0, t1=10.0, bin_width=2.0).bin_edges() 141 => array([0.0, 2.0, 4.0, 6.0, 8.0, 10.0]) 142 """ 143 num_edges = self.num_bins + 1 144 edges = np.arange(self.t0, self.t0 + num_edges * self.bin_width, self.bin_width) 145 146 # Ensure exactly num_edges (for safety in rare floating-point cases) 147 if len(edges) > num_edges: 148 edges = edges[:num_edges] 149 return edges
Return an array of bin edge times from t0 to t1, spaced by bin_width.
The result has length num_bins + 1 and is safe against floating-point rounding
by capping the range to include exactly the number of bins implied by num_bins().
Contract:
- Returns
num_bins + 1edge values such that: edges = [t0, t0 + bin_width, ..., t1]
Guarantees: bin_start(k) == edges[k] bin_end(k) == edges[k + 1]
Handles floating-point rounding safely: If np.arange overproduces due to rounding, result is trimmed to ensure exactly
num_bins + 1entries.
This method defines the canonical bin boundaries used across the presence matrix and all derived metrics.
Example:
Timescale(t0=0.0, t1=10.0, bin_width=2.0).bin_edges() => array([0.0, 2.0, 4.0, 6.0, 8.0, 10.0])
152 def time_range(self, bin_idx: int) -> Tuple[float, float]: 153 """ 154 Return the (start, end) time of a bin. 155 Contract: 156 Returns tuple (bin_start(k), bin_end(k)) 157 Matches exactly the continuous interval spanned by the bin 158 """ 159 return self.bin_start(bin_idx), self.bin_end(bin_idx)
Return the (start, end) time of a bin.
Contract:
Returns tuple (bin_start(k), bin_end(k)) Matches exactly the continuous interval spanned by the bin
15@dataclass 16class PresenceMap: 17 """ 18 A PresenceMap maps a continuous presence interval [start, end) 19 onto a discrete time grid defined by a Timescale. 20 21 The result is a bin-aligned representation: 22 - `start_bin` is the index of the first bin touched 23 - `end_bin` is the exclusive upper bound (i.e., first bin not touched) 24 - `start_value` and `end_value` represent fractional presence at the edges 25 - Bins between `start_bin` and `end_bin` are fully or partially covered 26 27 Contract: 28 - A presence is considered "mapped" if it overlaps the timescale [t0, t1) 29 - Mapped presences always produce: 30 start_bin ∈ [0, num_bins) 31 end_bin ∈ (start_bin, num_bins] 32 - The bin range [start_bin, end_bin) contains all and only the bins the presence overlaps 33 - start_value ∈ (0.0, 1.0] if partially covers `start_bin` 34 - end_value ∈ (0.0, 1.0] if partially covers `end_bin - 1` 35 """ 36 37 presence: PresenceAssertion 38 """The presence entry""" 39 time_scale: Timescale 40 """The time scale that the presence is mapped to""" 41 42 is_mapped: bool 43 """True if the presence has a valid mapping. Unmapped presences have value=-1 44 for start_slice, end_slice, start_value and end_value. 45 """ 46 47 start_bin: int 48 """The starting bin in the discrete mapping""" 49 end_bin: int 50 """The ending bin in the discrete mapping` 51 of row `row`. 52 """ 53 start_value: float 54 """A presence value 0 < p < 1.0 that represents a potentially partial presence at the start of the mapping""" 55 end_value: float 56 """A presence value 0 < p < 1.0 that represents a potentially partial presence at the end of the mapping""" 57 58 @property 59 def bin_range(self) -> range: 60 return range(self.start_bin, self.end_bin) if self.is_mapped else range(0) 61 62 @property 63 def duration(self) -> float: 64 return self.presence.reset_time - self.presence.onset_time 65 66 67 def __init__(self, presence: PresenceAssertion, time_scale: Timescale): 68 """ 69 Map a presence interval to matrix slice indices and edge fractional values 70 using the provided Timescale object. 71 """ 72 self.presence = presence 73 self.time_scale = time_scale 74 ts = self.time_scale 75 is_mapped = False 76 start_bin = -1 77 end_bin = -1 78 start_value = -1.0 79 end_value = -1.0 80 81 if presence.overlaps(ts.t0, ts.t1): 82 is_mapped = True 83 start_bin, end_bin = ts.bin_slice(presence.onset_time, presence.reset_time) 84 start_value, end_value = self._compute_fractional_values(presence.onset_time, start_bin, presence.reset_time, end_bin) 85 86 self.is_mapped = is_mapped 87 self.start_bin = start_bin 88 self.end_bin = end_bin 89 self.start_value = start_value 90 self.end_value = end_value 91 92 def _compute_fractional_values(self, start_time: float, start_bin: int, end_time: float, end_bin: int): 93 ts = self.time_scale 94 # Compute partial overlap at start bin 95 start_value = ts.fractional_overlap(start_time, end_time, start_bin) 96 97 # Compute partial overlap at end bin, if not same as start 98 if end_bin - 1 > start_bin: 99 end_value = ts.fractional_overlap(start_time, end_time, end_bin - 1) 100 else: 101 end_value = 0.0 102 103 return start_value, end_value 104 105 106 def is_active(self, start_bin: int, end_bin: int): 107 return end_bin > self.start_bin and start_bin < self.end_bin 108 109 def presence_value_in(self, start_time: float, end_time: float) -> float: 110 """ 111 Computes total presence value (in time) within [start_time, end_time), 112 using bin-based approximation logic, clipped to the given interval. 113 """ 114 ts = self.time_scale 115 bin_width = ts.bin_width 116 117 start_bin, end_bin = ts.bin_slice(start_time, end_time) 118 if self.is_mapped and self.is_active(start_bin, end_bin): 119 # Clip window to actual presence bounds 120 effective_start = max(self.presence.onset_time, start_time) 121 effective_end = min(self.presence.reset_time, end_time) 122 123 effective_start_bin, effective_end_bin = ts.bin_slice(effective_start, effective_end) 124 125 if start_time == ts.t0 and end_time == ts.t1: 126 start_value = self.start_value 127 end_value = self.end_value 128 else: 129 start_value, end_value = self._compute_fractional_values(effective_start, effective_start_bin, effective_end, effective_end_bin) 130 131 full_bin_value = max(0, effective_end_bin - effective_start_bin - 2) 132 133 fractional_value = start_value + end_value 134 135 return (full_bin_value + fractional_value) * bin_width 136 else: 137 return 0.0 138 139 @property 140 def presence_value(self) -> float: 141 return self.presence_value_in(self.time_scale.t0, self.time_scale.t1)
A PresenceMap maps a continuous presence interval [start, end) onto a discrete time grid defined by a Timescale.
The result is a bin-aligned representation:
start_binis the index of the first bin touchedend_binis the exclusive upper bound (i.e., first bin not touched)start_valueandend_valuerepresent fractional presence at the edges- Bins between
start_binandend_binare fully or partially covered
Contract:
- A presence is considered "mapped" if it overlaps the timescale [t0, t1)
- Mapped presences always produce: start_bin ∈ [0, num_bins) end_bin ∈ (start_bin, num_bins]
- The bin range [start_bin, end_bin) contains all and only the bins the presence overlaps
- start_value ∈ (0.0, 1.0] if partially covers
start_bin - end_value ∈ (0.0, 1.0] if partially covers
end_bin - 1
67 def __init__(self, presence: PresenceAssertion, time_scale: Timescale): 68 """ 69 Map a presence interval to matrix slice indices and edge fractional values 70 using the provided Timescale object. 71 """ 72 self.presence = presence 73 self.time_scale = time_scale 74 ts = self.time_scale 75 is_mapped = False 76 start_bin = -1 77 end_bin = -1 78 start_value = -1.0 79 end_value = -1.0 80 81 if presence.overlaps(ts.t0, ts.t1): 82 is_mapped = True 83 start_bin, end_bin = ts.bin_slice(presence.onset_time, presence.reset_time) 84 start_value, end_value = self._compute_fractional_values(presence.onset_time, start_bin, presence.reset_time, end_bin) 85 86 self.is_mapped = is_mapped 87 self.start_bin = start_bin 88 self.end_bin = end_bin 89 self.start_value = start_value 90 self.end_value = end_value
Map a presence interval to matrix slice indices and edge fractional values using the provided Timescale object.
True if the presence has a valid mapping. Unmapped presences have value=-1 for start_slice, end_slice, start_value and end_value.
A presence value 0 < p < 1.0 that represents a potentially partial presence at the start of the mapping
A presence value 0 < p < 1.0 that represents a potentially partial presence at the end of the mapping
109 def presence_value_in(self, start_time: float, end_time: float) -> float: 110 """ 111 Computes total presence value (in time) within [start_time, end_time), 112 using bin-based approximation logic, clipped to the given interval. 113 """ 114 ts = self.time_scale 115 bin_width = ts.bin_width 116 117 start_bin, end_bin = ts.bin_slice(start_time, end_time) 118 if self.is_mapped and self.is_active(start_bin, end_bin): 119 # Clip window to actual presence bounds 120 effective_start = max(self.presence.onset_time, start_time) 121 effective_end = min(self.presence.reset_time, end_time) 122 123 effective_start_bin, effective_end_bin = ts.bin_slice(effective_start, effective_end) 124 125 if start_time == ts.t0 and end_time == ts.t1: 126 start_value = self.start_value 127 end_value = self.end_value 128 else: 129 start_value, end_value = self._compute_fractional_values(effective_start, effective_start_bin, effective_end, effective_end_bin) 130 131 full_bin_value = max(0, effective_end_bin - effective_start_bin - 2) 132 133 fractional_value = start_value + end_value 134 135 return (full_bin_value + fractional_value) * bin_width 136 else: 137 return 0.0
Computes total presence value (in time) within [start_time, end_time), using bin-based approximation logic, clipped to the given interval.
18class PresenceMatrix: 19 """ 20 A scale-invariant, optionally lazy matrix representation of element presences over discrete time bins. 21 22 Each row corresponds to a single `Presence`, and each column represents a discrete time bin defined by a `Timescale`. 23 The matrix records the degree of presence of each element within a given boundary over time, where each value is a real number in [0.0, 1.0]: 24 - 1.0 = full presence for the duration of the time bin 25 - 0.0 = no presence 26 - values in between represent partial presence due to overlap 27 28 The matrix can be computed eagerly via `materialize()` or accessed lazily through NumPy-style slicing. 29 30 ### Structure 31 32 - **Rows:** Each row corresponds to one `Presence` instance. 33 - **Columns:** Each column represents a discrete bin of time defined by the `Timescale` (from `t0` to `t1` using `bin_width`). 34 - The matrix shape is therefore `(len(presences), timescale.num_bins)`. 35 36 ### Usage 37 38 ```python 39 from pcalc import PresenceMatrix 40 from metamodel.timescale import Timescale 41 42 # Define a time window with bin width of 1.0 43 ts = Timescale(t0=0.0, t1=5.0, bin_width=1.0) 44 45 # Construct lazily 46 matrix = PresenceMatrix(presences, time_scale=ts) 47 48 # Access entire row 49 row = matrix[0] # row 0 as 1D array 50 51 # Access single value 52 value = matrix[2, 3] # presence at row 2, column 3 53 54 # Access slice of row 55 window = matrix[1, 1:4] # row 1, columns 1–3 56 57 # Access slice of rows 58 rows = matrix[0:2] # rows 0 and 1 59 60 # Access single column 61 col = matrix[:, 2] # all rows at column 2 62 63 # Access column block 64 col_block = matrix[:, 1:4] # all rows, columns 1–3 65 66 # Materialize full matrix (optional) 67 dense = matrix.materialize() 68 ``` 69 70 Features 71 -------- 72 - Lazy evaluation by default; full matrix computed only if needed 73 - NumPy-style indexing: supports full rows, row/column slicing, and scalar access 74 - Precision-preserving: partial bin overlaps are retained in the matrix 75 - Compatible with matrix operations and flow metric calculations 76 - Backed by a sparse `PresenceMap`, which stores slice indices and fractional overlaps 77 78 Notes 79 ----- 80 - Use `materialize()` if you want to extract or operate on the full dense matrix 81 - Use `matrix[i, j]`, `matrix[i, j:k]`, or `matrix[:, j]` for lightweight slicing without allocating the full matrix 82 - Stepped slicing (e.g., `matrix[::2]`) is not currently supported 83 84""" 85 86 def __init__(self, presences: List[PresenceAssertion], time_scale: Timescale, materialize=False): 87 """ 88 Construct a presence matrix from a list of Presences and time window configuration. 89 90 Args: 91 presences: A list of `Presence` instances, one per element of interest. 92 time_scale: The discrete `Timescale` that the matrix will be normalized to. 93 materialize: If True, immediately constructs the full backing matrix. 94 Otherwise, matrix values will be computed on demand using the sparse presence map. 95 """ 96 97 self.presence_matrix: Optional[npt.NDArray[np.float64]] = None 98 """ 99 A real valued matrix with shape (num_Presences, num_bins). 100 When every presence.start and presence.end are whole numbers every value 101 in the matrix is either 0.0 or 1.0. If they are not whole numbers, the presence 102 is mapped to a number between 0.0 and 1.0 at the start and end (or both), with any 103 intermediate value being 1.0. 104 """ 105 106 self.time_scale = time_scale 107 """ 108 The time scale of the presence matrix. 109 """ 110 111 self.presence_map: List[PresenceMap] = [] 112 self.shape = None 113 self.init_presence_map(presences) 114 115 if materialize: 116 self.materialize() 117 118 def init_presence_map(self, presences: List[PresenceAssertion]) -> None: 119 """ 120 Initialize the internal presence matrix based on the Presence intervals and binning scheme. 121 Only presences that overlap the timescale endpoints [t0, t1) are mapped. 122 """ 123 ts = self.time_scale # Timescale object: includes t0, t1, bin_width 124 125 for row, presence in enumerate(presences): 126 presence_map = PresenceMap(presence, ts) 127 if presence_map.is_mapped: 128 self.presence_map.append(presence_map) 129 130 num_bins = ts.num_bins 131 num_rows = len(self.presence_map) 132 self.shape = (num_rows, num_bins) 133 134 def is_materialized(self) -> bool: 135 """Return True if the backing matrix has been materialized.""" 136 return self.presence_matrix is not None 137 138 def materialize(self) -> npt.NDArray[np.float64]: 139 """ 140 Materialize and return the full presence matrix from presence maps. 141 If already materialized, this is a no-op and returns the cached matrix. 142 143 Use this only if want the full matrix to operate on. For most cases, you should 144 be able to work with the sparse representation with the presence map and using 145 array slicing on the matrix object. So think twice about why you are materializing 146 a matrix. 147 148 Returns: 149 The dense presence matrix of shape (num_presences, num_bins). 150 """ 151 if self.is_materialized(): 152 return self.presence_matrix 153 154 num_rows, num_cols = self.shape 155 matrix = np.zeros((num_rows, num_cols), dtype=float) 156 157 for row, pm in enumerate(self.presence_map): 158 if not pm.is_mapped: 159 continue 160 start = pm.start_bin 161 end = pm.end_bin 162 matrix[row, start] = pm.start_value 163 if end - 1 > start: 164 matrix[row, end - 1] = pm.end_value 165 if end - start > 2: 166 matrix[row, start + 1: end - 1] = 1.0 167 168 self.presence_matrix = matrix 169 return self.presence_matrix 170 171 def drop_materialization(self) -> None: 172 """Discard the cached matrix, returning to sparse-only mode.""" 173 self.presence_matrix = None 174 175 def _compute_row_slice(self, row: int, start: int, stop: int) -> np.ndarray: 176 """ 177 On-demand computation of a row slice from presence map. 178 If the presence is not mapped or out of bounds, returns zeroes. 179 """ 180 pm = self.presence_map[row] 181 width = stop - start 182 output = np.zeros(width, dtype=float) 183 184 if not pm.is_mapped: 185 return output 186 187 # Slice and overlap window 188 for col in range(start, stop): 189 if col < pm.start_bin or col >= pm.end_bin: 190 continue 191 elif col == pm.start_bin: 192 output[col - start] = pm.start_value 193 elif col == pm.end_bin - 1: 194 output[col - start] = pm.end_value 195 else: 196 output[col - start] = 1.0 197 198 return output 199 200 @property 201 def presences(self) -> List[PresenceAssertion]: 202 return [pm.presence for pm in self.presence_map] 203 204 def __getitem__(self, index): 205 """ 206 Support NumPy-style indexing: 207 - matrix[i] → row i 208 - matrix[i:j] → row slice (returns 2D array) 209 - matrix[i, j] → scalar 210 - matrix[i, j:k] → row[i], column slice 211 - matrix[:, j] → column j (all rows) 212 - matrix[:, j:k] → column block j:k (all rows) 213 """ 214 # matrix[i:j] → top-level row slicing 215 if isinstance(index, slice): 216 if index.step is not None: 217 raise ValueError("PresenceMatrix does not support slicing with a step.") 218 start = index.start if index.start is not None else 0 219 stop = index.stop if index.stop is not None else self.shape[0] 220 if self.presence_matrix is not None: 221 return self.presence_matrix[start:stop] 222 return np.array([self[row] for row in range(start, stop)]) 223 224 # matrix[i, j], matrix[i, j:k], matrix[:, j] 225 if isinstance(index, tuple): 226 row_idx, col_idx = index 227 228 # matrix[:, j] or matrix[:, j:k] 229 if isinstance(row_idx, slice): 230 if row_idx.step is not None: 231 raise ValueError("PresenceMatrix does not support stepped row slicing.") 232 row_start = row_idx.start if row_idx.start is not None else 0 233 row_stop = row_idx.stop if row_idx.stop is not None else self.shape[0] 234 235 if isinstance(col_idx, int): 236 return np.array([self[row, col_idx] for row in range(row_start, row_stop)]) 237 238 elif isinstance(col_idx, slice): 239 if col_idx.step is not None: 240 raise ValueError("PresenceMatrix does not support stepped column slicing.") 241 col_start = col_idx.start if col_idx.start is not None else 0 242 col_stop = col_idx.stop if col_idx.stop is not None else self.shape[1] 243 return np.array([self[row, col_start:col_stop] for row in range(row_start, row_stop)]) 244 245 # matrix[i, j] or matrix[i, j:k] 246 elif isinstance(row_idx, int): 247 if isinstance(col_idx, int): 248 return self.presence_matrix[row_idx, col_idx] if self.presence_matrix is not None \ 249 else self._compute_row_slice(row_idx, col_idx, col_idx + 1)[0] 250 251 elif isinstance(col_idx, slice): 252 if col_idx.step is not None: 253 raise ValueError("PresenceMatrix does not support stepped column slicing.") 254 start = col_idx.start if col_idx.start is not None else 0 255 stop = col_idx.stop if col_idx.stop is not None else self.shape[1] 256 return self.presence_matrix[row_idx, start:stop] if self.presence_matrix is not None \ 257 else self._compute_row_slice(row_idx, start, stop) 258 259 # matrix[i] → single row 260 if isinstance(index, int): 261 return self.presence_matrix[index] if self.presence_matrix is not None \ 262 else self._compute_row_slice(index, 0, self.shape[1]) 263 264 raise TypeError(f"Invalid index for PresenceMatrix: {index}")
A scale-invariant, optionally lazy matrix representation of element presences over discrete time bins.
Each row corresponds to a single Presence, and each column represents a discrete time bin defined by a Timescale.
The matrix records the degree of presence of each element within a given boundary over time, where each value is a real number in [0.0, 1.0]:
- 1.0 = full presence for the duration of the time bin
- 0.0 = no presence
- values in between represent partial presence due to overlap
The matrix can be computed eagerly via materialize() or accessed lazily through NumPy-style slicing.
Structure
- Rows: Each row corresponds to one
Presenceinstance. - Columns: Each column represents a discrete bin of time defined by the
Timescale(fromt0tot1usingbin_width). - The matrix shape is therefore
(len(presences), timescale.num_bins).
Usage
from pcalc import PresenceMatrix
from metamodel.timescale import Timescale
# Define a time window with bin width of 1.0
ts = Timescale(t0=0.0, t1=5.0, bin_width=1.0)
# Construct lazily
matrix = PresenceMatrix(presences, time_scale=ts)
# Access entire row
row = matrix[0] # row 0 as 1D array
# Access single value
value = matrix[2, 3] # presence at row 2, column 3
# Access slice of row
window = matrix[1, 1:4] # row 1, columns 1–3
# Access slice of rows
rows = matrix[0:2] # rows 0 and 1
# Access single column
col = matrix[:, 2] # all rows at column 2
# Access column block
col_block = matrix[:, 1:4] # all rows, columns 1–3
# Materialize full matrix (optional)
dense = matrix.materialize()
Features
- Lazy evaluation by default; full matrix computed only if needed
- NumPy-style indexing: supports full rows, row/column slicing, and scalar access
- Precision-preserving: partial bin overlaps are retained in the matrix
- Compatible with matrix operations and flow metric calculations
- Backed by a sparse
PresenceMap, which stores slice indices and fractional overlaps
Notes
- Use
materialize()if you want to extract or operate on the full dense matrix - Use
matrix[i, j],matrix[i, j:k], ormatrix[:, j]for lightweight slicing without allocating the full matrix - Stepped slicing (e.g.,
matrix[::2]) is not currently supported
86 def __init__(self, presences: List[PresenceAssertion], time_scale: Timescale, materialize=False): 87 """ 88 Construct a presence matrix from a list of Presences and time window configuration. 89 90 Args: 91 presences: A list of `Presence` instances, one per element of interest. 92 time_scale: The discrete `Timescale` that the matrix will be normalized to. 93 materialize: If True, immediately constructs the full backing matrix. 94 Otherwise, matrix values will be computed on demand using the sparse presence map. 95 """ 96 97 self.presence_matrix: Optional[npt.NDArray[np.float64]] = None 98 """ 99 A real valued matrix with shape (num_Presences, num_bins). 100 When every presence.start and presence.end are whole numbers every value 101 in the matrix is either 0.0 or 1.0. If they are not whole numbers, the presence 102 is mapped to a number between 0.0 and 1.0 at the start and end (or both), with any 103 intermediate value being 1.0. 104 """ 105 106 self.time_scale = time_scale 107 """ 108 The time scale of the presence matrix. 109 """ 110 111 self.presence_map: List[PresenceMap] = [] 112 self.shape = None 113 self.init_presence_map(presences) 114 115 if materialize: 116 self.materialize()
Construct a presence matrix from a list of Presences and time window configuration.
Arguments:
- presences: A list of
Presenceinstances, one per element of interest. - time_scale: The discrete
Timescalethat the matrix will be normalized to. - materialize: If True, immediately constructs the full backing matrix. Otherwise, matrix values will be computed on demand using the sparse presence map.
A real valued matrix with shape (num_Presences, num_bins). When every presence.start and presence.end are whole numbers every value in the matrix is either 0.0 or 1.0. If they are not whole numbers, the presence is mapped to a number between 0.0 and 1.0 at the start and end (or both), with any intermediate value being 1.0.
118 def init_presence_map(self, presences: List[PresenceAssertion]) -> None: 119 """ 120 Initialize the internal presence matrix based on the Presence intervals and binning scheme. 121 Only presences that overlap the timescale endpoints [t0, t1) are mapped. 122 """ 123 ts = self.time_scale # Timescale object: includes t0, t1, bin_width 124 125 for row, presence in enumerate(presences): 126 presence_map = PresenceMap(presence, ts) 127 if presence_map.is_mapped: 128 self.presence_map.append(presence_map) 129 130 num_bins = ts.num_bins 131 num_rows = len(self.presence_map) 132 self.shape = (num_rows, num_bins)
Initialize the internal presence matrix based on the Presence intervals and binning scheme. Only presences that overlap the timescale endpoints [t0, t1) are mapped.
134 def is_materialized(self) -> bool: 135 """Return True if the backing matrix has been materialized.""" 136 return self.presence_matrix is not None
Return True if the backing matrix has been materialized.
138 def materialize(self) -> npt.NDArray[np.float64]: 139 """ 140 Materialize and return the full presence matrix from presence maps. 141 If already materialized, this is a no-op and returns the cached matrix. 142 143 Use this only if want the full matrix to operate on. For most cases, you should 144 be able to work with the sparse representation with the presence map and using 145 array slicing on the matrix object. So think twice about why you are materializing 146 a matrix. 147 148 Returns: 149 The dense presence matrix of shape (num_presences, num_bins). 150 """ 151 if self.is_materialized(): 152 return self.presence_matrix 153 154 num_rows, num_cols = self.shape 155 matrix = np.zeros((num_rows, num_cols), dtype=float) 156 157 for row, pm in enumerate(self.presence_map): 158 if not pm.is_mapped: 159 continue 160 start = pm.start_bin 161 end = pm.end_bin 162 matrix[row, start] = pm.start_value 163 if end - 1 > start: 164 matrix[row, end - 1] = pm.end_value 165 if end - start > 2: 166 matrix[row, start + 1: end - 1] = 1.0 167 168 self.presence_matrix = matrix 169 return self.presence_matrix
Materialize and return the full presence matrix from presence maps. If already materialized, this is a no-op and returns the cached matrix.
Use this only if want the full matrix to operate on. For most cases, you should be able to work with the sparse representation with the presence map and using array slicing on the matrix object. So think twice about why you are materializing a matrix.
Returns:
The dense presence matrix of shape (num_presences, num_bins).
171 def drop_materialization(self) -> None: 172 """Discard the cached matrix, returning to sparse-only mode.""" 173 self.presence_matrix = None
Discard the cached matrix, returning to sparse-only mode.
15class PresenceInvariantDiscrete: 16 """ 17 **A finite, scale-invariant, non-equilibrium version of Little's Law.** 18 19 This class computes the components of The Presence Invariant of a presence matrix. 20 21 The Presence Invariant states that for any *finite* interval `[start_time, end_time)` over the timescale `[t0, t1)` 22 of a presence matrix, the following invariant condition holds. 23 24 $$ 25 L = \Lambda \cdot w 26 $$ 27 where 28 29 - **$L$**: the average *presence* per unit time in the interval (see `avg_presence_per_unit_time`). 30 - **$\Lambda$**: The *flow rate* - a finite approximation of *presence arrival/departure rate* (see `flow_rate`). 31 - **$w$**: The *residence time* - a finite approximation of *presence duration* (see `metamodel.presence.Presence.duration`). 32 33 This invariant extends the classical formulation of Little’s Law, an equilibrium-based identity, by establishing a 34 conservation law (of presence) that remains valid across arbitrary timescales, and in non-linear, stochastic processes 35 that operate far from equilibrium. 36 37 It holds unconditionally for any presence matrix and finite window, and serves as a foundational 38 construct for reasoning about flow in non-linear systems. 39 40 The proof of this invariant is surprisingly simple and elementary. 41 42 **Derivation:** 43 44 45 46 Let $A$ be the total presence in the matrix over a finite time window `[start_time, end_time)` of $T$ time units. 47 Let $N$ be the number of distinct presences that overlap the window. 48 49 Let $R(p_i)$ be the portion of the duration of $p_i$ that overlaps the window. This is the *residence time* of $p_i$ in the window. 50 51 The following diagram shows these quantities and the derivation. 52 53 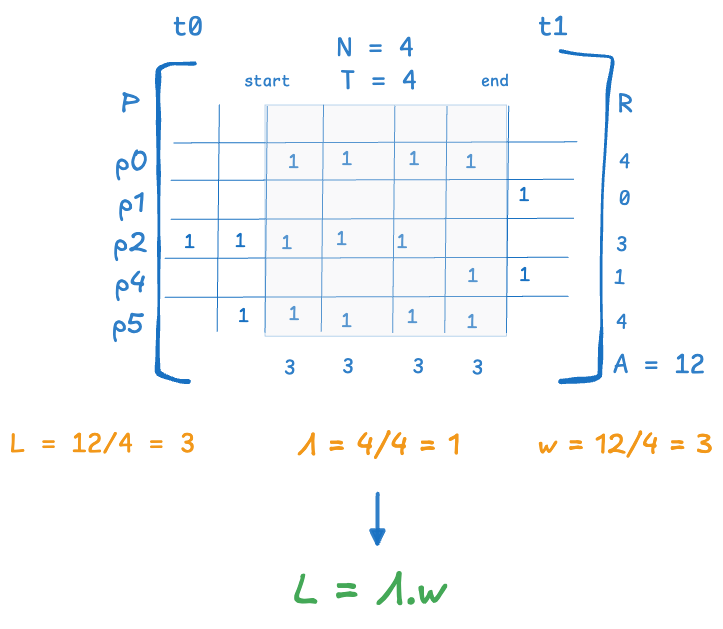 54 55 Then: 56 57 $$ 58 A = \sum_{i=1}^{N} R(p_i) 59 $$ 60 represents the sum of the elements in the presence matrix that foll in the time window `[start_time, end_time)`. 61 62 $A = 12$ presence-time-units in our example. 63 64 Average presence per unit time (see `avg_presence_per_unit_time`) is then: 65 66 $$ 67 L = A/T 68 $$ 69 70 $L = 3$ presences/time-unit in our example. 71 72 $w = $ Average residence time (see `avg_residence_time`) is then: 73 74 $$ 75 w = A/N 76 $$ 77 78 $w=3 time units per presence in our example. 79 80 We will define the flow rate as (see `flow_rate`): 81 82 $$ 83 \Lambda = N/T 84 $$ 85 86 $\Lambda = 1$ presence per time unit in our example. 87 88 Combining these: 89 90 $$ 91 L = A/T = A/N \cdot N/T = N/T \cdot A/N = \Lambda \cdot w 92 $$ 93 94 So we get 95 96 $$ 97 L = \Lambda \cdot w 98 $$ 99 100 101 This identity—what we call the *Presence Invariant*—is equivalent to a fundamental construct used in 102 all proofs of Little’s Law [1], and in particular, to one used by Stidham [2] to give a deterministic 103 proof of Little's Law [3] (see `flow_rate`). 104 105 Both the classical and the current presence-based versions are instances of *Rate Conservation Laws* 106 (as described by Miyazawa [3]). 107 108 However, the conserved quantities differ <sup>[1](#fn1)</sup>: 109 110 - In classical Little’s Law, $L = \lambda \cdot W$ holds *at equilibrium*, using long run arrival/departure rate $\lambda$ and 111 average presence duration $W$. 112 - In the Presence Invariant, $L = \Lambda \cdot w$ holds *universally*, where $\Lambda$ and $w$ are finite window 113 *approximations* of true arrival/departure rate and presence duration. 114 115 Stidham [2] proved the relationship between the quantities in the two versions and showed that 116 the classical form of Little’s Law emerges as a limiting case of the finite-window identity 117 *provided* the system approaches equilibrium as the window grows larger - ie the system is *convergent* in the long run. 118 119 If the system is *divergent* in the long run, at least one of the three quantities grows without limit and 120 the conservation law in the classical version does not hold. 121 122 However, the presence invariant continues to hold regardless of whether the system is convergent or divergent. 123 More details can be found under `flow_rate` and `avg_residence_time`. 124 125 Since non-linear systems rarely reach or maintain equilibrium, the Presence Invariant provides a more robust 126 and widely applicable conservation construct for causal reasoning about flow in such systems. 127 128 <small> 129 <a name="fn1"><strong>[1]</strong></a> 130 Note that we have lowercase $\lambda$ and uppercase $W$ in the classical law, and uppercase $\Lambda$ and 131 lowercase $w$ in the finite-window version, whereas $L$ remains the same in both. 132 133 This reflects the fact that in the Presence Invariant, $\Lambda$ is an overestimate of $\lambda$, and $w$ 134 is an underestimate of $W$. Both identities refer to the *same* observable construct for $L$. 135 </small> 136 137 ## References 138 139 1. **Little’s Law** 140 Little, J. D. C. (2011). *Little’s Law as viewed on its 50th anniversary*. MIT. 141 [https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf](https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf) 142 143 2. **Stidham's Proof of Little's Law** 144 Stidham, Shaler. Jr, *A last word on $L = \lambda \cdot W$*.Cornell University. 145 [https://pubsonline.informs.org/doi/epdf/10.1287/opre.22.2.417] 146 147 3. **Miyazawa on Rate Conservation Laws** 148 Miyazawa, M. (1994). *Rate conservation laws: a survey*. Science University of Tokyo. 149 [https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf](https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf) 150 151 152 """ 153 def __init__(self, matrix: PresenceMatrix): 154 self.matrix = matrix 155 """""" 156 self.presences: list[PresenceAssertion] = matrix.presences 157 """Only presences that overlap the interval [t0, t1) are included in Presence Metrics. 158 Note however that this may include presences that started before the interval or ended after the interval.""" 159 160 self.presence_map: list[PresenceMap] = matrix.presence_map 161 """Only presences that overlap the interval [t0, t1) are included in Presence Metrics. 162 Note however that this may include presences that started before the interval or ended after the interval.""" 163 164 self.ts = matrix.time_scale 165 """The timescale of the presence matrix. This is the default 'window' over which all metrics are computed.""" 166 167 def _resolve_range(self, start_time: Optional[float], end_time: Optional[float]) -> tuple[float, float]: 168 start = start_time if start_time is not None else self.ts.t0 169 end = end_time if end_time is not None else self.ts.t1 170 if start_time < self.ts.t0 or end_time > self.ts.t1: 171 raise ValueError( 172 f"Presence metrics are not defined outside the time scale of the presence matrix." 173 f"Time scale = [{self.ts.t0}, {self.ts.t1})." 174 f"Provided: [{start_time}, {end_time})" 175 ) 176 return start, end 177 178 179 def flow_rate(self, start_time: float = None, end_time: float = None) -> float: 180 """ 181 The flow rate Λ is defined as: 182 number of active presences in the matrix slice [:start_bin:end_bin] / 183 number of time bins in the slice (end_bin - start_bin) 184 185 Conceptually: 186 Let N be the number of presences (rows) that are active (non-zero) 187 in the matrix between start_time and end_time. 188 189 Let T be the number of discrete time bins (columns) in that interval. 190 191 Then: 192 flow_rate = Λ = N / T 193 194 Examples: 195 - If 4 presences span a 6-bin window, flow_rate = 4 / 6 = 0.666... 196 - If only one open-ended presence remains active over a 4-bin window, flow_rate = 1 / 4 = 0.25 197 198 The flow rate is a finite-window estimate of both long-run arrival rate and departure rate. 199 The precise relationship between flow rate, arrival rate, and departure rate is as follows: 200 201 N = number of presences that started *before* start_time (see `starting_presence_count`) 202 + number that started *in* the interval [start_time, end_time) (see `arrival_count`) 203 204 — this is also called the cumulative arrivals into the window 205 206 or equivalently: 207 208 N = number of presences that *ended* in [start_time, end_time) (see `departure_count`) 209 + number that ended *after* end_time (see `ending_presence_count`) 210 211 — this is the departure contribution from the window 212 213 These two decompositions of N are always equal; they just reflect different 214 ways of expressing the same set of active presences. 215 216 Intuitively, over a long enough window, if flow converges, most presences 217 will start and end within the window, with fewer presences that partially overlap 218 the interval at the beginning and end. 219 220 This makes N an (over) estimate of true arrivals or departures over that interval. 221 222 In other words, if flow through the boundary is asymptotically convergent over [start_time, end_time), 223 then: 224 flow_rate → arrival_rate → departure_rate 225 226 When flow is fully convergent over the interval, then: 227 flow_rate = arrival_rate = departure_rate 228 229 This equality is one of the key conditions for *stable* flow through the boundary. 230 231 On the other hand, if flow is not convergent over the interval, the delta between 232 flow rate, arrival rate, and departure rate will be large — either increasing (divergent) 233 or decreasing (convergent) over time. 234 """ 235 _, number_of_presences, num_bins = self.get_presence_summary(start_time, end_time) 236 return number_of_presences/num_bins if num_bins > 0 else 0.0 237 238 def avg_residence_time(self, start_time: float = None, end_time: float = None) -> float: 239 """ 240 Computes the average residence time over the interval [start_time, end_time). 241 242 Let \$ P \$ be the set of presences that overlap the interval \$[\\text{start\\_time}, \\text{end\\_time})\$. 243 244 The *residence time* \$ R(p) \$ is the time that presence \$ p \\in P \$ is active (overlaps) within that interval. 245 246 Presence is computed using bin-weighted overlap, so contributions may be fractional if presences only 247 partially cover a bin. 248 249 The average residence time \$ w \$ is given by: 250 251 \$$ 252 w = \\frac{\\sum_{p \\in P} R(p)}{|P|} 253 \$$ 254 255 If no presences are active in the interval, \$ w = 0.0 \$. 256 257 Note: 258 There are four possible ways a presence can overlap a window [start, end): 259 260 Ticks: 0 1 2 3 4 5 6 7 261 |---|---|---|---|---|---|---| 262 Window: |-----------| 263 264 Case 1: Fully inside 265 [=======] 266 267 Case 2: Starts before, ends inside 268 [=========== 269 270 Case 3: Starts inside, ends after 271 ===========] 272 273 Case 4: Fully spans window 274 [====================] 275 276 In all but Case 1, the window clips the presence, so the residence time 277 is smaller than the presence duration. In Case 1, residence time equals presence duration. 278 279 Intuitively, over a long enough window, if flow converges, most presences 280 will start and end within the window (Case 1), with fewer presences that partially overlap 281 the interval at the beginning and end or span the window (Cases 2–4). 282 283 This makes \$ w \$ an (under)estimate of true presence duration. 284 285 In other words, if flow through the boundary is asymptotically convergent over [start_time, end_time), 286 then: 287 residence time → presence duration. 288 289 When flow is fully convergent over the interval: 290 residence time = presence duration. 291 292 On the other hand, if flow is not convergent over the interval, the delta between 293 residence time and presence duration will be large — either increasing (divergent) 294 or decreasing (convergent) over time. 295 """ 296 total_presence_value, number_of_presences, _ = self.get_presence_summary(start_time, end_time) 297 return total_presence_value / number_of_presences if number_of_presences > 0 else 0.0 298 299 def avg_presence_per_unit_time(self, start_time: float = None, end_time: float = None) -> float: 300 """ 301 Computes the average presence per time bin over the interval [start_time, end_time). 302 303 Let \$ B \$ be the set of discrete time bins that cover the interval \$[\\text{start\\_time}, \\text{end\\_time})\$, 304 and let \$ P(b) \$ denote the total presence across all presences within each bin \$ b \\in B \$. 305 306 The average presence \$ L \$ is given by: 307 308 \$$ 309 L = \\frac{\\sum_{b \\in B} P(b)}{|B|} 310 \$$ 311 312 If the interval spans no bins, \$ L = 0.0 \$. 313 314 Note: 315 This is equivalent to computing the total presence by summing across rows (i.e., sum of all active presence 316 durations we used to compute residence time) divided by the number of bins in the interval. 317 318 Presence is computed using bin-weighted overlap, so contributions may be fractional if presences only 319 partially cover a bin. 320 321 Visually, this corresponds to summing presence *vertically* across bins: 322 323 Example: presences over time bins 324 325 Ticks: 0 1 2 3 4 326 |---|---|---|---| 327 P1: [=======] 328 P2: [=======] 329 P3: [=======] 330 331 Time bin 1: 332 ↑ (bin index 1 = [1, 2)) 333 |---| 334 P1: + 335 P2: + 336 P3: - 337 --------- 338 Sum: 2 339 340 So: 341 - Bin 1 has total presence = 2 342 - If we consider bins 1 to 3 (i.e., [1, 4)), and total presence = 5.5 343 - Then \$ L = 5.5 / 3 = 1.833... \$ 344 345 Conceptually, \$ L \$ reflects the average "load" or concurrency of presence in the system during the interval. 346 347 This metric is the time-relative (per unit time) complements the element-relative residence time \$ w \$. 348 """ 349 total_presence_value, _, num_bins = self.get_presence_summary(start_time, end_time) 350 return total_presence_value / num_bins if num_bins > 0 else 0.0 351 352 def get_presence_summary(self, start_time: float = None, end_time: float = None) -> Tuple[float, float, float]: 353 """ 354 Computes the three core quantities from which all presence-based metrics are derived: 355 356 - Total presence time \$ A \$ over the interval \$[\\text{start\\_time}, \\text{end\\_time})\$ 357 - Number of active presences \$ N \$ (i.e., rows overlapping the interval) 358 - Number of time bins \$ T \$ covering the interval 359 360 These three values form the basis for computing: 361 362 - Average presence per time bin: \$ L = A / T \$ 363 - Average residence time per presence: \$ w = A / N \$ 364 - Flow rate: \$ \\Lambda = N / T \$ 365 366 This method is the common workhorse that underlies `avg_presence_per_time_bin`, 367 `avg_residence_time_per_presence`, and `flow_rate`. 368 369 ... and much of this work lives in `PresenceMap.presence_value_in` 370 """ 371 start, end = self._resolve_range(start_time, end_time) 372 start_bin, end_bin = self.ts.bin_slice(start, end) 373 total_presence_value = 0 374 number_of_presences = 0 375 for pm in self.presence_map: 376 if pm.is_active(start_bin, end_bin): 377 total_presence_value += pm.presence_value_in(start_time, end_time) 378 number_of_presences += 1 379 380 return total_presence_value, number_of_presences, end_bin - start_bin 381 382 def get_presence_metrics(self, start_time: float = None, end_time: float = None) -> Tuple[float, float, float]: 383 """ 384 Computes all three components of the *Presence Invariant* for a finite window 385 $[ \text{start\_time}, \text{end\_time} )$ within the timescale $[ t_0, t_1 )$ 386 of the PresenceMatrix. 387 388 The Presence Invariant states that for *any* such interval: 389 390 $$ 391 L = \Lambda \cdot w 392 $$ 393 394 This invariant holds unconditionally and forms the foundation for reasoning about flow 395 in non-linear systems—systems that often operate far from equilibrium. It generalizes 396 the more familiar equilibrium-based Little’s Law by expressing a conservation law 397 that applies across all time scales. 398 399 - $L$: the *actual* average presence per unit time in the interval (this is not an approximation) 400 - $\Lambda$: the *finite approximation* of presence arrival rate (flow rate) 401 - $w$: the *finite approximation* of presence duration (residence time) 402 403 **Derivation:** 404 405 Let $ A $ be the total presence (i.e., the sum of active elements) in the matrix over the window. 406 Then: 407 408 $$ 409 A = \sum_{\text{rows}} \text{row totals} = \sum_{\text{columns}} \text{column totals} 410 $$ 411 412 Let $ N $ be the number of distinct presences in the window, and $ T $ the window length. 413 414 Then: 415 416 $$ 417 L = \frac{A}{T} = \frac{A}{N} \cdot \frac{N}{T} = w \cdot \Lambda 418 $$ 419 420 Hence: 421 422 $$ 423 L = \Lambda \cdot w 424 $$ 425 426 This identity—what we call the *Presence Invariant*—is a fundamental lemma used in 427 all proofs of Little’s Law [1], and can be seen as its finite-window specialization. 428 429 Both the classical and presence-based versions are instances of *Rate Conservation Laws* 430 (as described by Miyazawa [2]). However, the conserved parameters differ: 431 432 - In classical Little’s Law, $L = \lambda \cdot W$ holds *at equilibrium*, using true arrival rate $\lambda$ and average duration $W$. 433 - In the Presence Invariant, $L = \Lambda \cdot w$ holds *universally*, where $\Lambda$ and $w$ are finite approximations. 434 435 Since non-linear systems rarely reach or maintain equilibrium, the Presence Invariant provides a more robust 436 and widely applicable conservation principle for causal reasoning about flow in such systems. 437 438 ## References 439 440 1. **Little’s Law** 441 Little, J. D. C. (2011). *Little’s Law as viewed on its 50th anniversary*. MIT. 442 [https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf](https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf) 443 444 2. **Miyazawa on Rate Conservation Laws** 445 Miyazawa, M. (1994). *Rate conservation laws: a survey*. Science University of Tokyo. 446 [https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf](https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf) 447 448 """ 449 total_presence_value, number_of_presences, num_bins = self.get_presence_summary(start_time, end_time) 450 451 L = total_presence_value / num_bins if num_bins > 0 else 0.0 452 Λ = number_of_presences / num_bins if num_bins > 0 else 0.0 453 W = total_presence_value / number_of_presences if number_of_presences > 0 else 0.0 454 455 return L, Λ, W 456 457 458 459 460 def starting_presence_count(self, start_time: float = None, end_time: float = None) -> int: 461 start, end = self._resolve_range(start_time, end_time) 462 start_bin, end_bin = self.ts.bin_slice(start, end) 463 464 return sum( 465 1 for pm in self.presence_map 466 if pm.is_active(start_bin, end_bin) 467 #Note: here we must explicitly check the un-clipped 468 # bin indices, since we are looking for end indices that fall outside the 469 # window and even the matrix. So pm.end_bin is not the right test here. 470 and self.ts.bin_index(pm.presence.onset_time) < start_bin 471 ) 472 473 def ending_presence_count(self, start_time: float = None, end_time: float = None) -> int: 474 start, end = self._resolve_range(start_time, end_time) 475 start_bin, end_bin = self.ts.bin_slice(start, end) 476 477 return sum( 478 1 for pm in self.presence_map 479 if pm.is_active(start_bin, end_bin) 480 and (np.isinf(pm.presence.reset_time) or 481 # Note: here we must explicitly check the un-clipped 482 # bin indices, since we are looking for end indices that fall outside the 483 # window and even the matrix. So pm.end_bin is not the right test here. 484 self.ts.bin_index(pm.presence.reset_time) >= end_bin) 485 ) 486 487 def arrival_count(self, start_time: float = None, end_time: float = None) -> int: 488 """The number of presences that started within the window""" 489 start, end = self._resolve_range(start_time, end_time) 490 start_bin, end_bin = self.ts.bin_slice(start, end) 491 492 return sum( 493 1 for pm in self.presence_map 494 if start_bin <= self.ts.bin_index(pm.presence.onset_time) < end_bin 495 ) 496 497 def departure_count(self, start_time: float = None, end_time: float = None) -> int: 498 start, end = self._resolve_range(start_time, end_time) 499 start_bin, end_bin = self.ts.bin_slice(start, end) 500 501 return sum( 502 1 for pm in self.presence_map 503 if np.isfinite(pm.presence.reset_time) 504 and pm.is_active(start_bin, end_bin) 505 and self.ts.bin_index(pm.presence.reset_time) in range(start_bin, end_bin) 506 ) 507 508 509 def foo(self): 510 r""" 511 The key function of this class is to precisely compute the components of key rate conserved quantities 512 tied to Presence under both equilibrium and non-equilibrium conditions. 513 514 The key relationship that matters here is the Presence Invariant, which is rate conservation law 515 for a PresenceMatrix under non-equilibrium condition. 516 517 The Presence Invariant states that for *any* finite interval [start_time, end_time) over the timescale [t0, t1) 518 of a Presence Matrix: 519 520 $$ 521 L = \Lambda \cdot w 522 $$ 523 524 - $L$: the *actual* average presence per unit time in the interval (this is not an approximation) 525 - $\Lambda$: a *finite approximation* of presence arrival rate (flow rate) 526 - $w$: a *finite approximation* of presence duration (residence time) 527 528 This invariant holds unconditionally and forms the foundation for reasoning about flow 529 in non-linear systems—systems that often operate far from equilibrium. It generalizes 530 the more familiar Little’s Law that holds under certain equilibrium conditions as a conservation law 531 that applies across all time scales and non-equilibrium conditions. 532 533 The proof of this invariant is surprisingly simple and elementary. 534 535 **Derivation:** 536 537 Let $ A $ be the total presence (i.e., the sum of active elements) in the matrix over the window. 538 Then: 539 540 $$ 541 A = \sum_{\text{rows}} \text{row totals} = \sum_{\text{columns}} \text{column totals} 542 $$ 543 544 Let $ N $ be the number of distinct presences in the window, and $ T $ the window length. 545 546 Then: 547 548 $$ 549 550 L = \frac{A}{T} = \frac{A}{N} \cdot \frac{N}{T} = w \cdot \Lambda 551 552 $$ 553 554 Hence: 555 556 $$ L = \Lambda \cdot w $$ 557 558 The *Presence Invariant*—is a fundamental lemma used in 559 all proofs of Little’s Law [1], and can be seen as its finite-window version. 560 561 Both the classical and presence-based versions are instances of *Rate Conservation Laws* 562 (as described by Miyazawa [2]). However, the conserved parameters differ: 563 564 - In classical Little’s Law, $L = \lambda \cdot W$ holds *at equilibrium*, using true arrival rate $\lambda$ 565 and average duration $W$. 566 - In the Presence Invariant, $L = \Lambda \cdot w$ holds *universally*, where $\Lambda$ and $w$ are finite 567 window approximations. 568 569 Since non-linear systems rarely reach or maintain equilibrium, the Presence Invariant provides a more robust 570 and widely applicable conservation principle for causal reasoning about flow in such systems. 571 572 References: 573 574 1. **Little’s Law** 575 Little, J. D. C. (2011). *Little’s Law as viewed on its 50th anniversary*. MIT. 576 [https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf](https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf) 577 578 2. **Miyazawa on Rate Conservation Laws** 579 Miyazawa, M. (1994). *Rate conservation laws: a survey*. Science University of Tokyo. 580 [https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf](https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf) 581 """
A finite, scale-invariant, non-equilibrium version of Little's Law.
This class computes the components of The Presence Invariant of a presence matrix.
The Presence Invariant states that for any finite interval [start_time, end_time) over the timescale [t0, t1)
of a presence matrix, the following invariant condition holds.
$$ L = \Lambda \cdot w $$ where
- $L$: the average presence per unit time in the interval (see
avg_presence_per_unit_time). - $\Lambda$: The flow rate - a finite approximation of presence arrival/departure rate (see
flow_rate). - $w$: The residence time - a finite approximation of presence duration (see
metamodel.presence.Presence.duration).
This invariant extends the classical formulation of Little’s Law, an equilibrium-based identity, by establishing a conservation law (of presence) that remains valid across arbitrary timescales, and in non-linear, stochastic processes that operate far from equilibrium.
It holds unconditionally for any presence matrix and finite window, and serves as a foundational construct for reasoning about flow in non-linear systems.
The proof of this invariant is surprisingly simple and elementary.
Derivation:
Let $A$ be the total presence in the matrix over a finite time window [start_time, end_time) of $T$ time units.
Let $N$ be the number of distinct presences that overlap the window.
Let $R(p_i)$ be the portion of the duration of $p_i$ that overlaps the window. This is the residence time of $p_i$ in the window.
The following diagram shows these quantities and the derivation.

Then:
$$
A = \sum_{i=1}^{N} R(p_i)
$$
represents the sum of the elements in the presence matrix that foll in the time window [start_time, end_time).
$A = 12$ presence-time-units in our example.
Average presence per unit time (see avg_presence_per_unit_time) is then:
$$ L = A/T $$
$L = 3$ presences/time-unit in our example.
$w = $ Average residence time (see avg_residence_time) is then:
$$ w = A/N $$
$w=3 time units per presence in our example.
We will define the flow rate as (see flow_rate):
$$ \Lambda = N/T $$
$\Lambda = 1$ presence per time unit in our example.
Combining these:
$$ L = A/T = A/N \cdot N/T = N/T \cdot A/N = \Lambda \cdot w $$
So we get
$$ L = \Lambda \cdot w $$
This identity—what we call the Presence Invariant—is equivalent to a fundamental construct used in
all proofs of Little’s Law [1], and in particular, to one used by Stidham [2] to give a deterministic
proof of Little's Law [3] (see flow_rate).
Both the classical and the current presence-based versions are instances of Rate Conservation Laws (as described by Miyazawa [3]).
However, the conserved quantities differ 1:
- In classical Little’s Law, $L = \lambda \cdot W$ holds at equilibrium, using long run arrival/departure rate $\lambda$ and average presence duration $W$.
- In the Presence Invariant, $L = \Lambda \cdot w$ holds universally, where $\Lambda$ and $w$ are finite window approximations of true arrival/departure rate and presence duration.
Stidham [2] proved the relationship between the quantities in the two versions and showed that the classical form of Little’s Law emerges as a limiting case of the finite-window identity provided the system approaches equilibrium as the window grows larger - ie the system is convergent in the long run.
If the system is divergent in the long run, at least one of the three quantities grows without limit and the conservation law in the classical version does not hold.
However, the presence invariant continues to hold regardless of whether the system is convergent or divergent.
More details can be found under flow_rate and avg_residence_time.
Since non-linear systems rarely reach or maintain equilibrium, the Presence Invariant provides a more robust and widely applicable conservation construct for causal reasoning about flow in such systems.
[1] Note that we have lowercase $\lambda$ and uppercase $W$ in the classical law, and uppercase $\Lambda$ and lowercase $w$ in the finite-window version, whereas $L$ remains the same in both. This reflects the fact that in the Presence Invariant, $\Lambda$ is an overestimate of $\lambda$, and $w$ is an underestimate of $W$. Both identities refer to the same observable construct for $L$.References
Little’s Law Little, J. D. C. (2011). Little’s Law as viewed on its 50th anniversary. MIT. https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf
Stidham's Proof of Little's Law Stidham, Shaler. Jr, A last word on $L = \lambda \cdot W$.Cornell University. [https://pubsonline.informs.org/doi/epdf/10.1287/opre.22.2.417]
Miyazawa on Rate Conservation Laws Miyazawa, M. (1994). Rate conservation laws: a survey. Science University of Tokyo. https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf
153 def __init__(self, matrix: PresenceMatrix): 154 self.matrix = matrix 155 """""" 156 self.presences: list[PresenceAssertion] = matrix.presences 157 """Only presences that overlap the interval [t0, t1) are included in Presence Metrics. 158 Note however that this may include presences that started before the interval or ended after the interval.""" 159 160 self.presence_map: list[PresenceMap] = matrix.presence_map 161 """Only presences that overlap the interval [t0, t1) are included in Presence Metrics. 162 Note however that this may include presences that started before the interval or ended after the interval.""" 163 164 self.ts = matrix.time_scale 165 """The timescale of the presence matrix. This is the default 'window' over which all metrics are computed."""
Only presences that overlap the interval [t0, t1) are included in Presence Metrics. Note however that this may include presences that started before the interval or ended after the interval.
Only presences that overlap the interval [t0, t1) are included in Presence Metrics. Note however that this may include presences that started before the interval or ended after the interval.
The timescale of the presence matrix. This is the default 'window' over which all metrics are computed.
179 def flow_rate(self, start_time: float = None, end_time: float = None) -> float: 180 """ 181 The flow rate Λ is defined as: 182 number of active presences in the matrix slice [:start_bin:end_bin] / 183 number of time bins in the slice (end_bin - start_bin) 184 185 Conceptually: 186 Let N be the number of presences (rows) that are active (non-zero) 187 in the matrix between start_time and end_time. 188 189 Let T be the number of discrete time bins (columns) in that interval. 190 191 Then: 192 flow_rate = Λ = N / T 193 194 Examples: 195 - If 4 presences span a 6-bin window, flow_rate = 4 / 6 = 0.666... 196 - If only one open-ended presence remains active over a 4-bin window, flow_rate = 1 / 4 = 0.25 197 198 The flow rate is a finite-window estimate of both long-run arrival rate and departure rate. 199 The precise relationship between flow rate, arrival rate, and departure rate is as follows: 200 201 N = number of presences that started *before* start_time (see `starting_presence_count`) 202 + number that started *in* the interval [start_time, end_time) (see `arrival_count`) 203 204 — this is also called the cumulative arrivals into the window 205 206 or equivalently: 207 208 N = number of presences that *ended* in [start_time, end_time) (see `departure_count`) 209 + number that ended *after* end_time (see `ending_presence_count`) 210 211 — this is the departure contribution from the window 212 213 These two decompositions of N are always equal; they just reflect different 214 ways of expressing the same set of active presences. 215 216 Intuitively, over a long enough window, if flow converges, most presences 217 will start and end within the window, with fewer presences that partially overlap 218 the interval at the beginning and end. 219 220 This makes N an (over) estimate of true arrivals or departures over that interval. 221 222 In other words, if flow through the boundary is asymptotically convergent over [start_time, end_time), 223 then: 224 flow_rate → arrival_rate → departure_rate 225 226 When flow is fully convergent over the interval, then: 227 flow_rate = arrival_rate = departure_rate 228 229 This equality is one of the key conditions for *stable* flow through the boundary. 230 231 On the other hand, if flow is not convergent over the interval, the delta between 232 flow rate, arrival rate, and departure rate will be large — either increasing (divergent) 233 or decreasing (convergent) over time. 234 """ 235 _, number_of_presences, num_bins = self.get_presence_summary(start_time, end_time) 236 return number_of_presences/num_bins if num_bins > 0 else 0.0
The flow rate Λ is defined as: number of active presences in the matrix slice [:start_bin:end_bin] / number of time bins in the slice (end_bin - start_bin)
Conceptually:
Let N be the number of presences (rows) that are active (non-zero) in the matrix between start_time and end_time.
Let T be the number of discrete time bins (columns) in that interval.
Then: flow_rate = Λ = N / T
Examples:
- If 4 presences span a 6-bin window, flow_rate = 4 / 6 = 0.666...
- If only one open-ended presence remains active over a 4-bin window, flow_rate = 1 / 4 = 0.25
The flow rate is a finite-window estimate of both long-run arrival rate and departure rate. The precise relationship between flow rate, arrival rate, and departure rate is as follows:
N = number of presences that started *before* start_time (see `starting_presence_count`)
+ number that started *in* the interval [start_time, end_time) (see `arrival_count`)
— this is also called the cumulative arrivals into the window
or equivalently:
N = number of presences that *ended* in [start_time, end_time) (see `departure_count`)
+ number that ended *after* end_time (see `ending_presence_count`)
— this is the departure contribution from the window
These two decompositions of N are always equal; they just reflect different
ways of expressing the same set of active presences.
Intuitively, over a long enough window, if flow converges, most presences will start and end within the window, with fewer presences that partially overlap the interval at the beginning and end.
This makes N an (over) estimate of true arrivals or departures over that interval.
In other words, if flow through the boundary is asymptotically convergent over [start_time, end_time), then: flow_rate → arrival_rate → departure_rate
When flow is fully convergent over the interval, then: flow_rate = arrival_rate = departure_rate
This equality is one of the key conditions for stable flow through the boundary.
On the other hand, if flow is not convergent over the interval, the delta between flow rate, arrival rate, and departure rate will be large — either increasing (divergent) or decreasing (convergent) over time.
238 def avg_residence_time(self, start_time: float = None, end_time: float = None) -> float: 239 """ 240 Computes the average residence time over the interval [start_time, end_time). 241 242 Let \$ P \$ be the set of presences that overlap the interval \$[\\text{start\\_time}, \\text{end\\_time})\$. 243 244 The *residence time* \$ R(p) \$ is the time that presence \$ p \\in P \$ is active (overlaps) within that interval. 245 246 Presence is computed using bin-weighted overlap, so contributions may be fractional if presences only 247 partially cover a bin. 248 249 The average residence time \$ w \$ is given by: 250 251 \$$ 252 w = \\frac{\\sum_{p \\in P} R(p)}{|P|} 253 \$$ 254 255 If no presences are active in the interval, \$ w = 0.0 \$. 256 257 Note: 258 There are four possible ways a presence can overlap a window [start, end): 259 260 Ticks: 0 1 2 3 4 5 6 7 261 |---|---|---|---|---|---|---| 262 Window: |-----------| 263 264 Case 1: Fully inside 265 [=======] 266 267 Case 2: Starts before, ends inside 268 [=========== 269 270 Case 3: Starts inside, ends after 271 ===========] 272 273 Case 4: Fully spans window 274 [====================] 275 276 In all but Case 1, the window clips the presence, so the residence time 277 is smaller than the presence duration. In Case 1, residence time equals presence duration. 278 279 Intuitively, over a long enough window, if flow converges, most presences 280 will start and end within the window (Case 1), with fewer presences that partially overlap 281 the interval at the beginning and end or span the window (Cases 2–4). 282 283 This makes \$ w \$ an (under)estimate of true presence duration. 284 285 In other words, if flow through the boundary is asymptotically convergent over [start_time, end_time), 286 then: 287 residence time → presence duration. 288 289 When flow is fully convergent over the interval: 290 residence time = presence duration. 291 292 On the other hand, if flow is not convergent over the interval, the delta between 293 residence time and presence duration will be large — either increasing (divergent) 294 or decreasing (convergent) over time. 295 """ 296 total_presence_value, number_of_presences, _ = self.get_presence_summary(start_time, end_time) 297 return total_presence_value / number_of_presences if number_of_presences > 0 else 0.0
Computes the average residence time over the interval [start_time, end_time).
Let \$ P \$ be the set of presences that overlap the interval \$[\text{start_time}, \text{end_time})\$.
The residence time \$ R(p) \$ is the time that presence \$ p \in P \$ is active (overlaps) within that interval.
Presence is computed using bin-weighted overlap, so contributions may be fractional if presences only partially cover a bin.
The average residence time \$ w \$ is given by:
\$$ w = \frac{\sum_{p \in P} R(p)}{|P|} \$$
If no presences are active in the interval, \$ w = 0.0 \$.
Note:
There are four possible ways a presence can overlap a window [start, end):
Ticks: 0 1 2 3 4 5 6 7 |---|---|---|---|---|---|---| Window: |-----------|
Case 1: Fully inside [=======]
Case 2: Starts before, ends inside [===========
Case 3: Starts inside, ends after ===========]
Case 4: Fully spans window [====================]
In all but Case 1, the window clips the presence, so the residence time is smaller than the presence duration. In Case 1, residence time equals presence duration.
Intuitively, over a long enough window, if flow converges, most presences will start and end within the window (Case 1), with fewer presences that partially overlap the interval at the beginning and end or span the window (Cases 2–4).
This makes \$ w \$ an (under)estimate of true presence duration.
In other words, if flow through the boundary is asymptotically convergent over [start_time, end_time), then: residence time → presence duration.
When flow is fully convergent over the interval: residence time = presence duration.
On the other hand, if flow is not convergent over the interval, the delta between residence time and presence duration will be large — either increasing (divergent) or decreasing (convergent) over time.
299 def avg_presence_per_unit_time(self, start_time: float = None, end_time: float = None) -> float: 300 """ 301 Computes the average presence per time bin over the interval [start_time, end_time). 302 303 Let \$ B \$ be the set of discrete time bins that cover the interval \$[\\text{start\\_time}, \\text{end\\_time})\$, 304 and let \$ P(b) \$ denote the total presence across all presences within each bin \$ b \\in B \$. 305 306 The average presence \$ L \$ is given by: 307 308 \$$ 309 L = \\frac{\\sum_{b \\in B} P(b)}{|B|} 310 \$$ 311 312 If the interval spans no bins, \$ L = 0.0 \$. 313 314 Note: 315 This is equivalent to computing the total presence by summing across rows (i.e., sum of all active presence 316 durations we used to compute residence time) divided by the number of bins in the interval. 317 318 Presence is computed using bin-weighted overlap, so contributions may be fractional if presences only 319 partially cover a bin. 320 321 Visually, this corresponds to summing presence *vertically* across bins: 322 323 Example: presences over time bins 324 325 Ticks: 0 1 2 3 4 326 |---|---|---|---| 327 P1: [=======] 328 P2: [=======] 329 P3: [=======] 330 331 Time bin 1: 332 ↑ (bin index 1 = [1, 2)) 333 |---| 334 P1: + 335 P2: + 336 P3: - 337 --------- 338 Sum: 2 339 340 So: 341 - Bin 1 has total presence = 2 342 - If we consider bins 1 to 3 (i.e., [1, 4)), and total presence = 5.5 343 - Then \$ L = 5.5 / 3 = 1.833... \$ 344 345 Conceptually, \$ L \$ reflects the average "load" or concurrency of presence in the system during the interval. 346 347 This metric is the time-relative (per unit time) complements the element-relative residence time \$ w \$. 348 """ 349 total_presence_value, _, num_bins = self.get_presence_summary(start_time, end_time) 350 return total_presence_value / num_bins if num_bins > 0 else 0.0
Computes the average presence per time bin over the interval [start_time, end_time).
Let \$ B \$ be the set of discrete time bins that cover the interval \$[\text{start_time}, \text{end_time})\$, and let \$ P(b) \$ denote the total presence across all presences within each bin \$ b \in B \$.
The average presence \$ L \$ is given by:
\$$ L = \frac{\sum_{b \in B} P(b)}{|B|} \$$
If the interval spans no bins, \$ L = 0.0 \$.
Note:
This is equivalent to computing the total presence by summing across rows (i.e., sum of all active presence durations we used to compute residence time) divided by the number of bins in the interval.
Presence is computed using bin-weighted overlap, so contributions may be fractional if presences only partially cover a bin.
Visually, this corresponds to summing presence vertically across bins:
Example: presences over time bins
Ticks: 0 1 2 3 4 |---|---|---|---| P1: [=======] P2: [=======] P3: [=======]
Time bin 1: ↑ (bin index 1 = [1, 2)) |---| P1: + P2: + P3: - --------- Sum: 2
So: - Bin 1 has total presence = 2 - If we consider bins 1 to 3 (i.e., [1, 4)), and total presence = 5.5 - Then \$ L = 5.5 / 3 = 1.833... \$
Conceptually, \$ L \$ reflects the average "load" or concurrency of presence in the system during the interval.
This metric is the time-relative (per unit time) complements the element-relative residence time \$ w \$.
352 def get_presence_summary(self, start_time: float = None, end_time: float = None) -> Tuple[float, float, float]: 353 """ 354 Computes the three core quantities from which all presence-based metrics are derived: 355 356 - Total presence time \$ A \$ over the interval \$[\\text{start\\_time}, \\text{end\\_time})\$ 357 - Number of active presences \$ N \$ (i.e., rows overlapping the interval) 358 - Number of time bins \$ T \$ covering the interval 359 360 These three values form the basis for computing: 361 362 - Average presence per time bin: \$ L = A / T \$ 363 - Average residence time per presence: \$ w = A / N \$ 364 - Flow rate: \$ \\Lambda = N / T \$ 365 366 This method is the common workhorse that underlies `avg_presence_per_time_bin`, 367 `avg_residence_time_per_presence`, and `flow_rate`. 368 369 ... and much of this work lives in `PresenceMap.presence_value_in` 370 """ 371 start, end = self._resolve_range(start_time, end_time) 372 start_bin, end_bin = self.ts.bin_slice(start, end) 373 total_presence_value = 0 374 number_of_presences = 0 375 for pm in self.presence_map: 376 if pm.is_active(start_bin, end_bin): 377 total_presence_value += pm.presence_value_in(start_time, end_time) 378 number_of_presences += 1 379 380 return total_presence_value, number_of_presences, end_bin - start_bin
Computes the three core quantities from which all presence-based metrics are derived:
- Total presence time \$ A \$ over the interval \$[\text{start_time}, \text{end_time})\$
- Number of active presences \$ N \$ (i.e., rows overlapping the interval)
- Number of time bins \$ T \$ covering the interval
These three values form the basis for computing:
- Average presence per time bin: \$ L = A / T \$
- Average residence time per presence: \$ w = A / N \$
- Flow rate: \$ \Lambda = N / T \$
This method is the common workhorse that underlies avg_presence_per_time_bin,
avg_residence_time_per_presence, and flow_rate.
... and much of this work lives in PresenceMap.presence_value_in
382 def get_presence_metrics(self, start_time: float = None, end_time: float = None) -> Tuple[float, float, float]: 383 """ 384 Computes all three components of the *Presence Invariant* for a finite window 385 $[ \text{start\_time}, \text{end\_time} )$ within the timescale $[ t_0, t_1 )$ 386 of the PresenceMatrix. 387 388 The Presence Invariant states that for *any* such interval: 389 390 $$ 391 L = \Lambda \cdot w 392 $$ 393 394 This invariant holds unconditionally and forms the foundation for reasoning about flow 395 in non-linear systems—systems that often operate far from equilibrium. It generalizes 396 the more familiar equilibrium-based Little’s Law by expressing a conservation law 397 that applies across all time scales. 398 399 - $L$: the *actual* average presence per unit time in the interval (this is not an approximation) 400 - $\Lambda$: the *finite approximation* of presence arrival rate (flow rate) 401 - $w$: the *finite approximation* of presence duration (residence time) 402 403 **Derivation:** 404 405 Let $ A $ be the total presence (i.e., the sum of active elements) in the matrix over the window. 406 Then: 407 408 $$ 409 A = \sum_{\text{rows}} \text{row totals} = \sum_{\text{columns}} \text{column totals} 410 $$ 411 412 Let $ N $ be the number of distinct presences in the window, and $ T $ the window length. 413 414 Then: 415 416 $$ 417 L = \frac{A}{T} = \frac{A}{N} \cdot \frac{N}{T} = w \cdot \Lambda 418 $$ 419 420 Hence: 421 422 $$ 423 L = \Lambda \cdot w 424 $$ 425 426 This identity—what we call the *Presence Invariant*—is a fundamental lemma used in 427 all proofs of Little’s Law [1], and can be seen as its finite-window specialization. 428 429 Both the classical and presence-based versions are instances of *Rate Conservation Laws* 430 (as described by Miyazawa [2]). However, the conserved parameters differ: 431 432 - In classical Little’s Law, $L = \lambda \cdot W$ holds *at equilibrium*, using true arrival rate $\lambda$ and average duration $W$. 433 - In the Presence Invariant, $L = \Lambda \cdot w$ holds *universally*, where $\Lambda$ and $w$ are finite approximations. 434 435 Since non-linear systems rarely reach or maintain equilibrium, the Presence Invariant provides a more robust 436 and widely applicable conservation principle for causal reasoning about flow in such systems. 437 438 ## References 439 440 1. **Little’s Law** 441 Little, J. D. C. (2011). *Little’s Law as viewed on its 50th anniversary*. MIT. 442 [https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf](https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf) 443 444 2. **Miyazawa on Rate Conservation Laws** 445 Miyazawa, M. (1994). *Rate conservation laws: a survey*. Science University of Tokyo. 446 [https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf](https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf) 447 448 """ 449 total_presence_value, number_of_presences, num_bins = self.get_presence_summary(start_time, end_time) 450 451 L = total_presence_value / num_bins if num_bins > 0 else 0.0 452 Λ = number_of_presences / num_bins if num_bins > 0 else 0.0 453 W = total_presence_value / number_of_presences if number_of_presences > 0 else 0.0 454 455 return L, Λ, W
Computes all three components of the Presence Invariant for a finite window $[ ext{start_time}, ext{end_time} )$ within the timescale $[ t_0, t_1 )$ of the PresenceMatrix.
The Presence Invariant states that for any such interval:
$$
L = \Lambda \cdot w
$$
This invariant holds unconditionally and forms the foundation for reasoning about flow in non-linear systems—systems that often operate far from equilibrium. It generalizes the more familiar equilibrium-based Little’s Law by expressing a conservation law that applies across all time scales.
- $L$: the actual average presence per unit time in the interval (this is not an approximation)
- $\Lambda$: the finite approximation of presence arrival rate (flow rate)
- $w$: the finite approximation of presence duration (residence time)
Derivation:
Let $ A $ be the total presence (i.e., the sum of active elements) in the matrix over the window. Then:
$$ A = \sum_{ ext{rows}} ext{row totals} = \sum_{ ext{columns}} ext{column totals} $$
Let $ N $ be the number of distinct presences in the window, and $ T $ the window length.
Then:
$$ L = rac{A}{T} = rac{A}{N} \cdot rac{N}{T} = w \cdot \Lambda $$
Hence:
$$ L = \Lambda \cdot w $$
This identity—what we call the Presence Invariant—is a fundamental lemma used in all proofs of Little’s Law [1], and can be seen as its finite-window specialization.
Both the classical and presence-based versions are instances of Rate Conservation Laws (as described by Miyazawa [2]). However, the conserved parameters differ:
- In classical Little’s Law, $L = \lambda \cdot W$ holds at equilibrium, using true arrival rate $\lambda$ and average duration $W$.
- In the Presence Invariant, $L = \Lambda \cdot w$ holds universally, where $\Lambda$ and $w$ are finite approximations.
Since non-linear systems rarely reach or maintain equilibrium, the Presence Invariant provides a more robust and widely applicable conservation principle for causal reasoning about flow in such systems.
References
1. **Little’s Law**
Little, J. D. C. (2011). *Little’s Law as viewed on its 50th anniversary*. MIT.
[https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf](https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf)
2. **Miyazawa on Rate Conservation Laws**
Miyazawa, M. (1994). *Rate conservation laws: a survey*. Science University of Tokyo.
[https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf](https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf)
460 def starting_presence_count(self, start_time: float = None, end_time: float = None) -> int: 461 start, end = self._resolve_range(start_time, end_time) 462 start_bin, end_bin = self.ts.bin_slice(start, end) 463 464 return sum( 465 1 for pm in self.presence_map 466 if pm.is_active(start_bin, end_bin) 467 #Note: here we must explicitly check the un-clipped 468 # bin indices, since we are looking for end indices that fall outside the 469 # window and even the matrix. So pm.end_bin is not the right test here. 470 and self.ts.bin_index(pm.presence.onset_time) < start_bin 471 )
473 def ending_presence_count(self, start_time: float = None, end_time: float = None) -> int: 474 start, end = self._resolve_range(start_time, end_time) 475 start_bin, end_bin = self.ts.bin_slice(start, end) 476 477 return sum( 478 1 for pm in self.presence_map 479 if pm.is_active(start_bin, end_bin) 480 and (np.isinf(pm.presence.reset_time) or 481 # Note: here we must explicitly check the un-clipped 482 # bin indices, since we are looking for end indices that fall outside the 483 # window and even the matrix. So pm.end_bin is not the right test here. 484 self.ts.bin_index(pm.presence.reset_time) >= end_bin) 485 )
487 def arrival_count(self, start_time: float = None, end_time: float = None) -> int: 488 """The number of presences that started within the window""" 489 start, end = self._resolve_range(start_time, end_time) 490 start_bin, end_bin = self.ts.bin_slice(start, end) 491 492 return sum( 493 1 for pm in self.presence_map 494 if start_bin <= self.ts.bin_index(pm.presence.onset_time) < end_bin 495 )
The number of presences that started within the window
497 def departure_count(self, start_time: float = None, end_time: float = None) -> int: 498 start, end = self._resolve_range(start_time, end_time) 499 start_bin, end_bin = self.ts.bin_slice(start, end) 500 501 return sum( 502 1 for pm in self.presence_map 503 if np.isfinite(pm.presence.reset_time) 504 and pm.is_active(start_bin, end_bin) 505 and self.ts.bin_index(pm.presence.reset_time) in range(start_bin, end_bin) 506 )
509 def foo(self): 510 r""" 511 The key function of this class is to precisely compute the components of key rate conserved quantities 512 tied to Presence under both equilibrium and non-equilibrium conditions. 513 514 The key relationship that matters here is the Presence Invariant, which is rate conservation law 515 for a PresenceMatrix under non-equilibrium condition. 516 517 The Presence Invariant states that for *any* finite interval [start_time, end_time) over the timescale [t0, t1) 518 of a Presence Matrix: 519 520 $$ 521 L = \Lambda \cdot w 522 $$ 523 524 - $L$: the *actual* average presence per unit time in the interval (this is not an approximation) 525 - $\Lambda$: a *finite approximation* of presence arrival rate (flow rate) 526 - $w$: a *finite approximation* of presence duration (residence time) 527 528 This invariant holds unconditionally and forms the foundation for reasoning about flow 529 in non-linear systems—systems that often operate far from equilibrium. It generalizes 530 the more familiar Little’s Law that holds under certain equilibrium conditions as a conservation law 531 that applies across all time scales and non-equilibrium conditions. 532 533 The proof of this invariant is surprisingly simple and elementary. 534 535 **Derivation:** 536 537 Let $ A $ be the total presence (i.e., the sum of active elements) in the matrix over the window. 538 Then: 539 540 $$ 541 A = \sum_{\text{rows}} \text{row totals} = \sum_{\text{columns}} \text{column totals} 542 $$ 543 544 Let $ N $ be the number of distinct presences in the window, and $ T $ the window length. 545 546 Then: 547 548 $$ 549 550 L = \frac{A}{T} = \frac{A}{N} \cdot \frac{N}{T} = w \cdot \Lambda 551 552 $$ 553 554 Hence: 555 556 $$ L = \Lambda \cdot w $$ 557 558 The *Presence Invariant*—is a fundamental lemma used in 559 all proofs of Little’s Law [1], and can be seen as its finite-window version. 560 561 Both the classical and presence-based versions are instances of *Rate Conservation Laws* 562 (as described by Miyazawa [2]). However, the conserved parameters differ: 563 564 - In classical Little’s Law, $L = \lambda \cdot W$ holds *at equilibrium*, using true arrival rate $\lambda$ 565 and average duration $W$. 566 - In the Presence Invariant, $L = \Lambda \cdot w$ holds *universally*, where $\Lambda$ and $w$ are finite 567 window approximations. 568 569 Since non-linear systems rarely reach or maintain equilibrium, the Presence Invariant provides a more robust 570 and widely applicable conservation principle for causal reasoning about flow in such systems. 571 572 References: 573 574 1. **Little’s Law** 575 Little, J. D. C. (2011). *Little’s Law as viewed on its 50th anniversary*. MIT. 576 [https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf](https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf) 577 578 2. **Miyazawa on Rate Conservation Laws** 579 Miyazawa, M. (1994). *Rate conservation laws: a survey*. Science University of Tokyo. 580 [https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf](https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf) 581 """
The key function of this class is to precisely compute the components of key rate conserved quantities tied to Presence under both equilibrium and non-equilibrium conditions.
The key relationship that matters here is the Presence Invariant, which is rate conservation law for a PresenceMatrix under non-equilibrium condition.
The Presence Invariant states that for any finite interval [start_time, end_time) over the timescale [t0, t1) of a Presence Matrix:
$$
L = \Lambda \cdot w
$$
- $L$: the *actual* average presence per unit time in the interval (this is not an approximation)
- $\Lambda$: a *finite approximation* of presence arrival rate (flow rate)
- $w$: a *finite approximation* of presence duration (residence time)
This invariant holds unconditionally and forms the foundation for reasoning about flow
in non-linear systems—systems that often operate far from equilibrium. It generalizes
the more familiar Little’s Law that holds under certain equilibrium conditions as a conservation law
that applies across all time scales and non-equilibrium conditions.
The proof of this invariant is surprisingly simple and elementary.
**Derivation:**
Let $ A $ be the total presence (i.e., the sum of active elements) in the matrix over the window.
Then:
$$
A = \sum_{\text{rows}} \text{row totals} = \sum_{\text{columns}} \text{column totals}
$$
Let $ N $ be the number of distinct presences in the window, and $ T $ the window length.
Then:
$$
L = \frac{A}{T} = \frac{A}{N} \cdot \frac{N}{T} = w \cdot \Lambda
$$
Hence:
$$ L = \Lambda \cdot w $$
The *Presence Invariant*—is a fundamental lemma used in
all proofs of Little’s Law [1], and can be seen as its finite-window version.
Both the classical and presence-based versions are instances of *Rate Conservation Laws*
(as described by Miyazawa [2]). However, the conserved parameters differ:
- In classical Little’s Law, $L = \lambda \cdot W$ holds *at equilibrium*, using true arrival rate $\lambda$
and average duration $W$.
- In the Presence Invariant, $L = \Lambda \cdot w$ holds *universally*, where $\Lambda$ and $w$ are finite
window approximations.
Since non-linear systems rarely reach or maintain equilibrium, the Presence Invariant provides a more robust
and widely applicable conservation principle for causal reasoning about flow in such systems.
References:
1. **Little’s Law**
Little, J. D. C. (2011). *Little’s Law as viewed on its 50th anniversary*. MIT.
[https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf](https://people.cs.umass.edu/~emery/classes/cmpsci691st/readings/OS/Littles-Law-50-Years-Later.pdf)
2. **Miyazawa on Rate Conservation Laws**
Miyazawa, M. (1994). *Rate conservation laws: a survey*. Science University of Tokyo.
[https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf](https://www.rs.tus.ac.jp/miyazawa/pdf-file/Miya1994-QS-RCL.pdf)